10. Sınıf Binom Açılımı Konu Anlatımı Matematik

Binom Açılımı Çözümlü Sorular

Binom Açılımı Video

Binom açılımı, (a + b)^n ifadesini genişletme işlemidir. Bu genişleme, her terimin birinci ve ikinci terimin üslerinin toplamının bir kuvveti olduğu bir toplam şeklinde ifade edilir. 10. sınıf matematik derslerinde binom açılımı, Pascal üçgeni ve kombinasyonlarla birlikte öğretilir.

(x + y)^n = x^n + nC1 x^(n - 1) y + nC2 x^(n - 2) y^2 + ... + nCn y^n

Bu formülde,

• x ve y, binomdaki terimlerdir.
• n, binomun derecesidir.
• nC1, n'in 1'e bölünmesiyle elde edilen sayıdır.
• nC2, n'in 2'ye bölünmesiyle elde edilen sayıdır.
• ...
• nCn, n'in n'e bölünmesiyle elde edilen sayıdır.

Binom Açılımı Örneği

(x + y)^2 formülünü Pascal üçgeni kullanarak açalım.

(x + y)^2 = x^2 + nC1 x y + nC2 y^2

Pascal üçgeninden, nC1 = 2 ve nC2 = 1 olduğunu buluyoruz. Bu değerlerle, formül şu şekilde olur:

(x + y)^2 = x^2 + 2x y + 1y^2

Bu formül, (x + y)^2 = x^2 + 2xy + y^2 ifadesine denk olur.
Binom Açılımı Çözümlü Sorular
1. Soru
(x + y)^3 formülünü açınız.
Çözüm
Pascal üçgeninden, nC1 = 3, nC2 = 3 ve nC3 = 1 olduğunu buluyoruz. Bu değerlerle, formül şu şekilde olur:

(x + y)^3 = x^3 + 3x^2 y + 3xy^2 + y^3

2. Soru

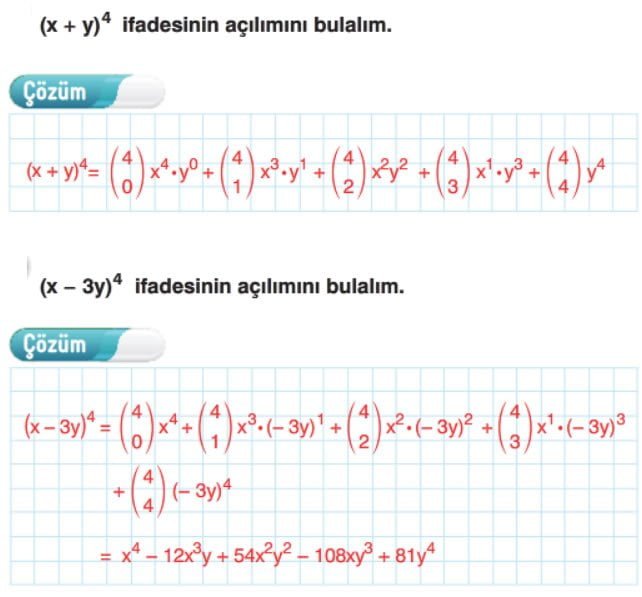
(x - y)^4 formülünü açınız.

Çözüm

Pascal üçgeninden, nC1 = 4, nC2 = 6, nC3 = 4 ve nC4 = 1 olduğunu buluyoruz. Bu değerlerle, formül şu şekilde olur:

(x - y)^4 = x^4 - 4x^3 y + 6x^2 y^2 - 4xy^3 + y^4

3. Soru
(2x + 3y)^5 formülünü açınız.
Çözüm
Pascal üçgeninden, nC1 = 5, nC2 = 10, nC3 = 10, nC4 = 5 ve nC5 = 1 olduğunu buluyoruz. Bu değerlerle, formül şu şekilde olur:

(2x + 3y)^5 = 32x^5 + 250x^4 y + 600x^3 y^2 + 750x^2 y^3 + 300xy^4 + 24y^5
Etkinlikler

1. Etkinlik: (x + y)^n formülünü açınız.

2. Etkinlik: (x - y)^n formülünü açınız.
3. Etkinlik: (ax + by)^n formülünü açınız.
Bu etkinlikleri çözerek, binom açılımını daha iyi anlayabilirsiniz
Binom Açılımı Kartları:

1. Öğrencilere $(x+x{)}^n$ tipi ifadeler içeren kartlar verin.
2. Her öğrenciye, karttaki ifadeyi genişletmelerini ve sadeleştirmelerini isteyin.
3. Sonuçları sınıfta paylaşarak farklı yöntemleri ve stratejileri tartışın.

Kombinatorik Sorular:

1. "Beş farklı renkte bir kutuda 3 top seçeceğiz.(a+b)³ ifadesini kullanarak kaç farklı renkte top seçebiliriz?"
2. "İki kitap arasından 4 kitap seçeceğiz. $(�+�{)}^4$ ifadesini kullanarak kaç farklı kitap seçebiliriz?"

Bu etkinlikler öğrencilere binom açılımını daha iyi anlamalarında yardımcı olabilir. Her bir öğrencinin kendi hızında çalışmasına ve birbirleriyle işbirliği yapmasına izin vermek önemlidir.