10. Sınıf Fonksiyon Grafikleri Konu Anlatımı ve Çözümlü Sorular Matematik

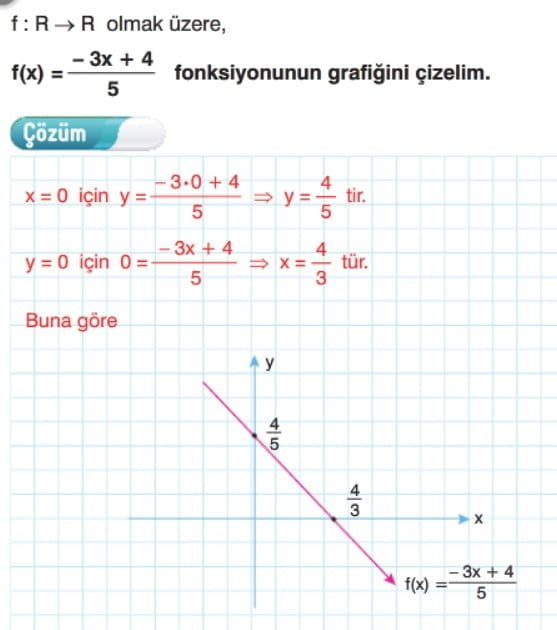
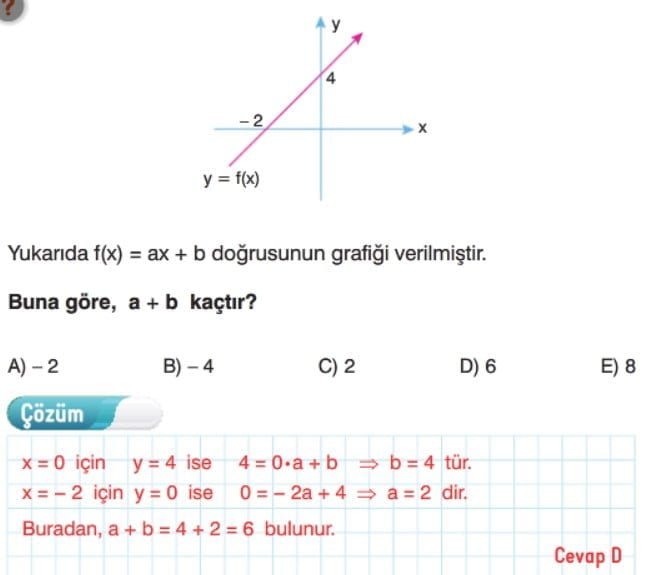
Doğrusal Fonksiyonların Grafiği

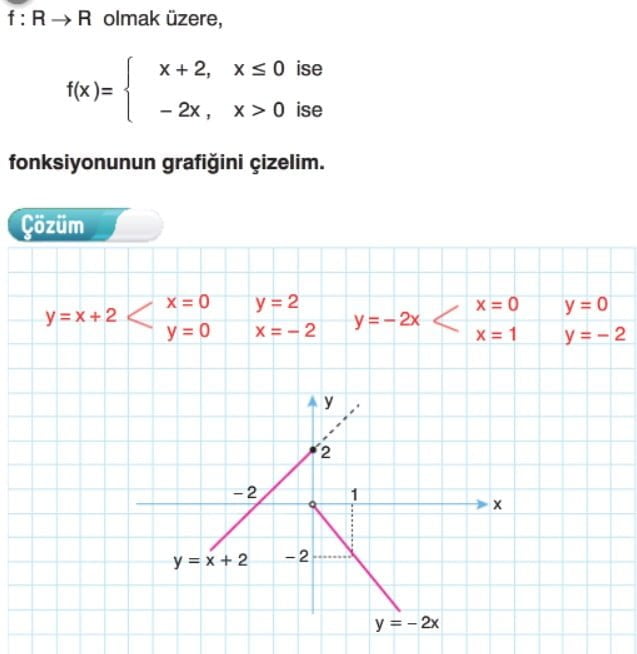
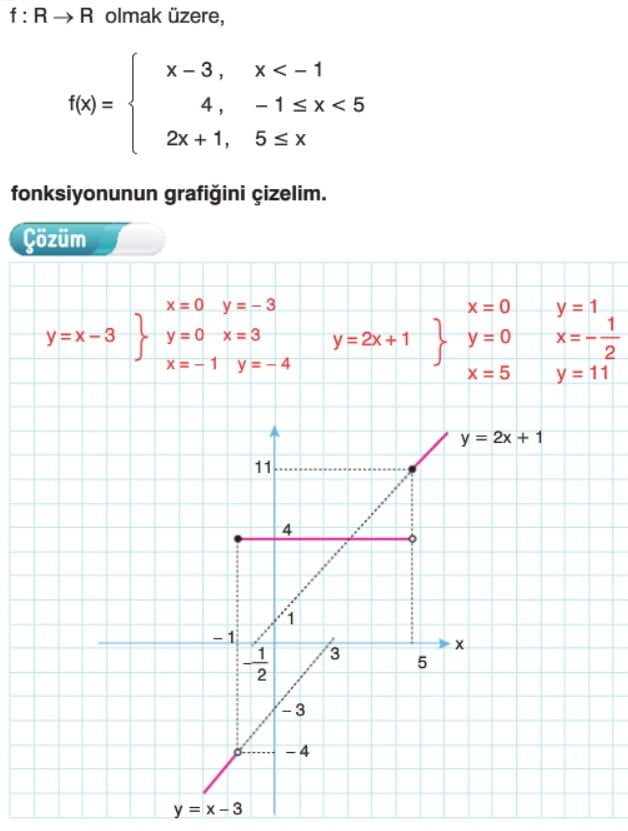
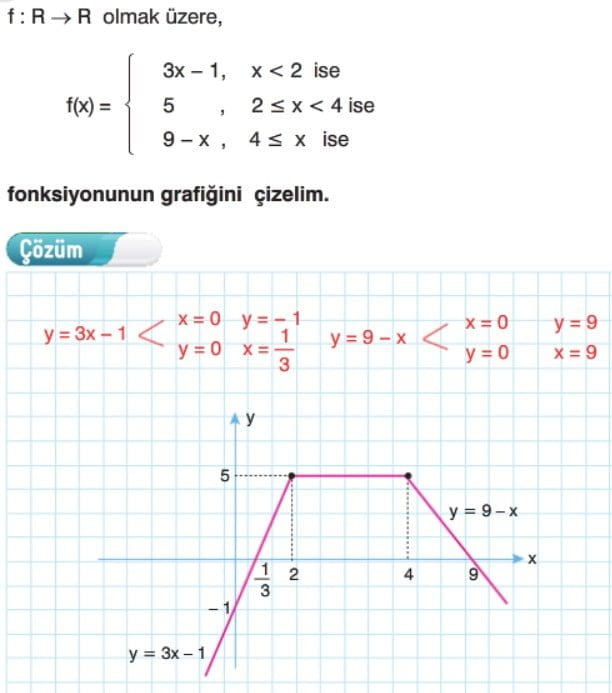
Parçalı Fonksiyonların Grafiği

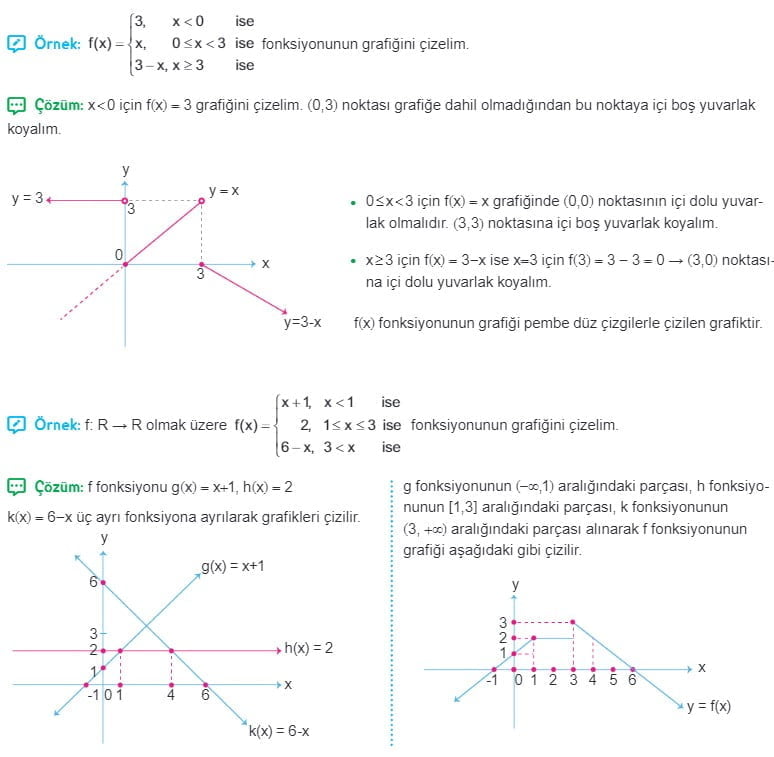
Grafik Üzerinden Tanım ve Görüntü Kümesi Bulma

Dikey Doğru Testi

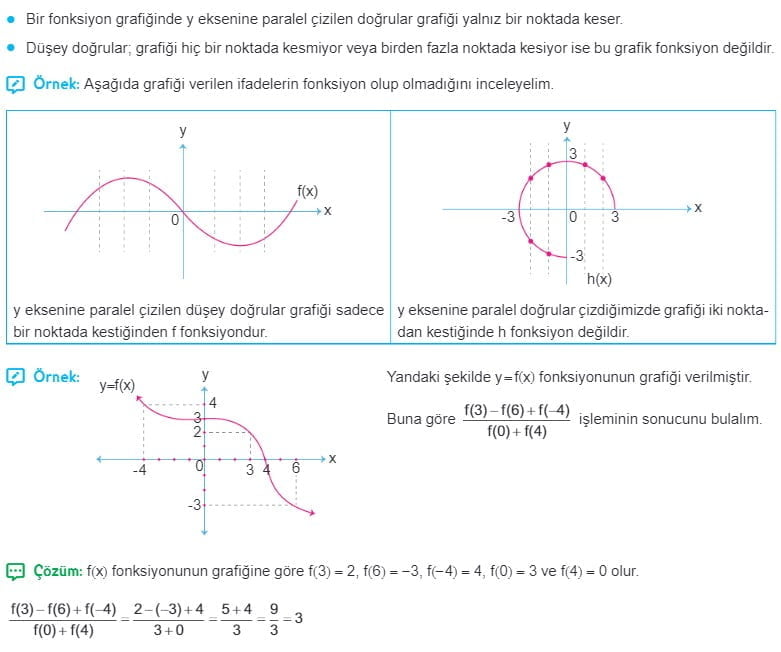
Yatay Doğru Testi

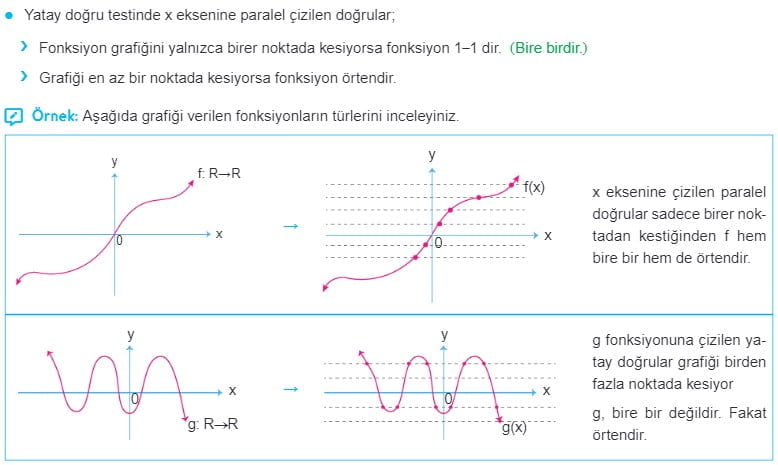
Fonksiyon Grafikleri İle İlgili Günlük Hayat Problemleri

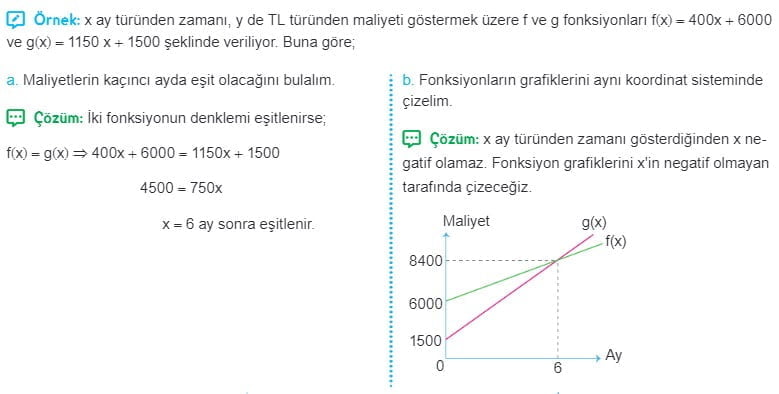
Fonksiyon Grafikleri Çözümlü Sorular

Fonksiyon Grafikleri Video

Fonksiyon grafikleri, bir fonksiyonun x-y düzlemindeki grafiğini gösteren çizimlerdir. Fonksiyon grafikleri, bir fonksiyonun özelliklerini incelemek ve fonksiyonla ilgili problemleri çözmek için kullanılır.

Fonksiyon grafiklerini çizmek için, öncelikle fonksiyonun tanım kümesini ve değer kümesini belirlememiz gerekir. Tanım kümesi, fonksiyonun tanımlandığı x değerlerinin kümesidir. Değer kümesi, fonksiyonun değer verdiği y değerlerinin kümesidir.

Fonksiyonun tanım ve değer kümelerini belirledikten sonra, fonksiyonun bir kaç x değeri için y değerlerini hesaplayabiliriz. Bu değerleri x-y düzleminde işaretleyerek, fonksiyonun grafiğini çizmeye başlayabiliriz.

Fonksiyon grafiklerini çizerken aşağıdaki adımları takip edebiliriz:

1. Fonksiyonun tanım ve değer kümesini belirleyin.
2. Fonksiyonun bir kaç x değeri için y değerlerini hesaplayın.
3. Bu değerleri x-y düzleminde işaretleyin.
4. Bu noktaları birleştirerek fonksiyonun grafiğini çizin.

Fonksiyon grafiklerinin temel özelliklerini şu şekilde özetleyebiliriz:

• Bir fonksiyonun grafiği, x-y düzleminde bir eğridir.
• Bir fonksiyonun grafiği, y-eksenini kestiği noktada, x değeri 0'dır.
• Bir fonksiyonun grafiği, x-eksenini kestiği noktada, y değeri fonksiyonun tanımsız olduğu bir değerdir.

Fonksiyon grafiklerinin özelliklerini kullanarak, fonksiyonla ilgili problemleri çözebiliriz. Örneğin, bir fonksiyonun bir noktadan geçen bir doğruya ait olup olmadığını, fonksiyonun bir noktaya yaklaşıp yaklaşmadığını, fonksiyonun bir noktadan geçen bir eğriye ait olup olmadığını, fonksiyonun bir noktadan geçen bir çembere ait olup olmadığını belirleyebiliriz.

Fonksiyon grafiklerinin bazı örnekleri şunlardır:

• Y = x fonksiyonunun grafiği, bir doğrudur.
• Y = x^2 fonksiyonunun grafiği, bir paraboldür.
• Y = e^x fonksiyonunun grafiği, bir üstel eğridir.
• Y = ln(x) fonksiyonunun grafiği, bir logaritma eğrisidir.

Fonksiyon grafikleri, matematikte önemli bir yere sahiptir. Fonksiyon grafiklerini çizmek ve özelliklerini incelemek, fonksiyonlarla ilgili problemleri çözmek için gereklidir.

Örnek Soru 1: Verilen f(x)=x2 +2x−3 fonksiyonunun grafiğini çizin ve en düşük noktasını belirleyin.

Çözüm:

• Fonksiyonun grafiğini çizerek, parabolün şeklini gözlemleyin.
• Parabolün en düşük noktasını belirlemek için x=−b/2a​ formülünü kullanın. Burada $a$ katsayısı 1, $$ katsayısı 2, $$ katsayısı -3'tir.
• En düşük noktanın $$ koordinatını bulduktan sonra, $$ fonksiyonunu kullanarak $$ koordinatını hesaplayın.

Örnek Soru 2: Verilen g(x)=1/x​ fonksiyonunun grafiğini çizin ve asimptotlarını belirleyin.

Çözüm:

• Grafikte $$ değerlerini büyüttükçe, $$ fonksiyonunun değerlerinin sıfıra yaklaştığını gözlemleyin. Bu durumu inceleyerek, $$ eksenine yaklaşan (0, 0) noktasını sıfır noktasına giden bir asimptot olarak tanımlayabilirsiniz.
• $g(x)$ fonksiyonu için $x=0$ noktasında dikey bir asimptot bulunur.