10. Sınıf Fonksiyon Kavramı ve Gösterimi Konu Anlatımı Matematik

Sonraki Konular

• Fonksiyon Çeşitleri (Parçalı Fonksiyon, Birim Fonksiyon, Sabit Fonksiyon, Doğrusal Fonksiyon, Eşit Fonksiyonlar, Tek ve Çift Fonksiyon, Bire Bir Fonksiyon, Örten ve İçine Fonksiyon)
• Fonksiyonlarda Dört İşlem
• Fonksiyon Grafikleri (Doğrusal Fonksiyonların Grafikleri, Parçalı Fonksiyonların Grafikleri, Yatay ve Dikey Doğru Testi, Grafikler ile İlgili Problemler)

Fonksiyon Kavramı

Fonksiyon Kavramı ve Gösterimi Çözümlü Sorular

Fonksiyon Kavramı ve Gösterimi Video

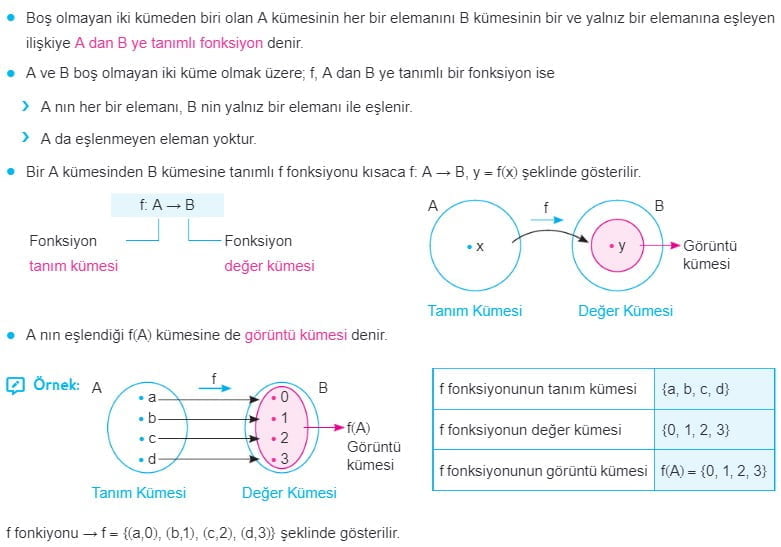
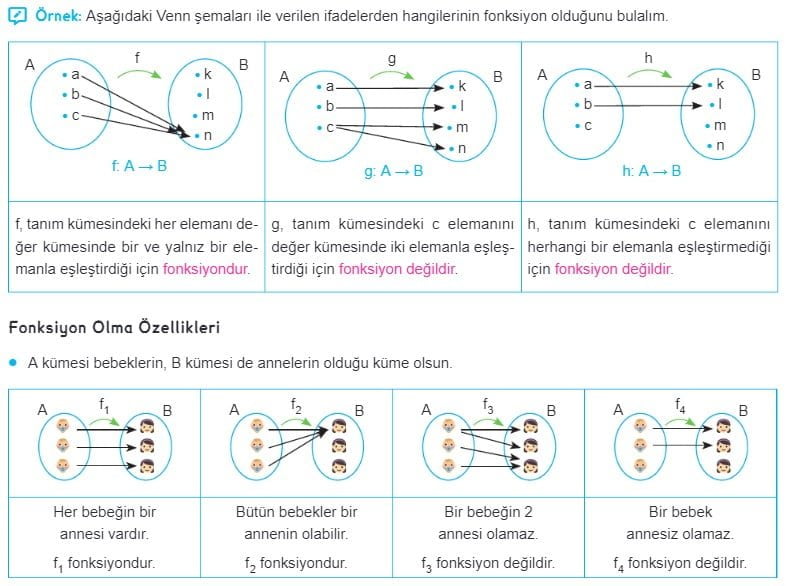
Matematikte, bir fonksiyon, bir kümedeki her elemanı başka bir kümedeki bir elemana eşleyen bir ilişkidir. Fonksiyonun tanım kümesi, fonksiyonun tanımlandığı kümedir. Fonksiyonun değer kümesi ise, fonksiyonun tanım kümesinde aldığı değerlerin oluşturduğu kümedir.

Örneğin, sıcaklık fonksiyonu, sıcaklık ölçümleri kümesini sıcaklık değerleri kümesine eşleyen bir ilişkidir. Sıcaklık ölçümleri kümesi, [-273, 5000] aralığındaki tüm gerçek sayıları içerir. Sıcaklık değerleri kümesi ise, [-273, 5000] aralığındaki tüm gerçek sayıları içerir.

Fonksiyonlar, matematikte çok yaygın olarak kullanılan bir kavramdır. Grafikler, denklemler, dönüşümler, olasılık teorisi, ekonomi ve mühendislik gibi birçok alanda fonksiyonlardan yararlanılır.

Fonksiyonların Özellikleri

Fonksiyonların, tanım kümesi ve değer kümesi dışında da bazı özellikleri vardır. Bu özellikler şunlardır:

• Tek Değerlilik: Bir fonksiyonun bir tanım kümesi elemanı için aldığı değer, tektir. Yani, bir fonksiyona ait bir x değeri için, f(x) değeri tektir.
• Artıklık: Bir fonksiyonun değer kümesi, tanım kümesinin alt kümesidir. Yani, bir fonksiyona ait bir x değeri için, f(x) değeri, x'in tanım kümesinde ise, f(x) değeri, x'in değer kümesinde de bulunur.
• İkili İşlemler: Fonksiyonların tanım kümesi ve değer kümesi üzerindeki ikili işlemler, fonksiyona da uygulanabilir.

Fonksiyon Türleri

Fonksiyonlar, tanım kümesi ve değer kümesi gibi özelliklerine göre çeşitli sınıflara ayrılabilir. Bu sınıflardan bazıları şunlardır:

• Sürekli Fonksiyonlar: Bir fonksiyonun tanım kümesi üzerindeki her x noktasında, f(x) değeri, x'in bir limitine eşittir.
• Discontinious Fonksiyonlar: Bir fonksiyonun tanım kümesi üzerindeki bazı x noktalarında, f(x) değeri, x'in bir limitine eşit değildir.
• Artan Fonksiyonlar: Bir fonksiyonun tanım kümesi üzerinde, x1 < x2 ise, f(x1) < f(x2) eşitliği her zaman sağlanır.
• Azalan Fonksiyonlar: Bir fonksiyonun tanım kümesi üzerinde, x1 < x2 ise, f(x1) > f(x2) eşitliği her zaman sağlanır.
• Birebir Fonksiyonlar: Bir fonksiyonun tanım kümesi üzerindeki her x1 ve x2 elemanı için, f(x1) = f(x2) eşitliği sağlanıyorsa ve x1 ≠ x2 ise, f(x) fonksiyonu birebirtir.
• Örten Fonksiyonlar: Bir fonksiyonun değer kümesi, tanım kümesinin her elemanına karşılık gelen bir değer içerir.

Fonksiyonlarda Dört İşlem

Fonksiyonlarda dört işlem, fonksiyonların tanım kümesi ve değer kümesi üzerindeki ikili işlemlere göre uygulanabilir.

• Toplama ve Çıkarma: Fonksiyonların tanım kümesi ve değer kümesi aynı ise, bu fonksiyonlar toplanabilir ve çıkarılabilir.
• Çarpma ve Bölme: Fonksiyonların tanım kümesi ve değer kümesi aynı ise ve bu fonksiyonlardan biri sürekli ise, bu fonksiyonlar çarpılabilir ve bölünebilir.

Fonksiyonlarda Uygulamalar

Fonksiyonlar, matematikte çok yaygın olarak kullanılan bir kavram olduğu için, birçok alanda uygulamaları vardır. Bu uygulamalardan bazıları şunlardır:

• Grafikler: Fonksiyonların grafikleri, fonksiyonların özelliklerini incelemek için kullanılır.
• Denklemler: Fonksiyonlar, denklemlerde bilinmeyen değerlerin yerlerini bulmak için kullanılır.
• Dönüşümler: Fonksiyonlar, grafiklerin ve denklemlerin özelliklerini değiştirmek için kullanılır.
• Olasılık Teorisi: Fonksiyonlar, olasılık teorisinde, olasılıkları hesaplamak için kullanılır.
• Ekonomi: Fonksiyonlar, ekonomide, ekonomik modelleri oluşturmak ve analiz etmek için kullanılır.

1. Soru: Tanım kümesi ve değer kümesi verilen bir fonksiyonun tek değerli olup olmadığını nasıl anlarız?

Cevap: Bir fonksiyonun tek değerli olup olmadığını anlamak için, fonksiyonun tanım kümesi üzerindeki her bir x elemanı için, f(x) değerinin tek olup olmadığını kontrol etmemiz gerekir. Eğer fonksiyonun tanım kümesi üzerindeki her bir x elemanı için, f(x) değeri tek ise, fonksiyon tek değerlidir. Örneğin, f(x) = 2x + 1 fonksiyonunun tanım kümesi, tüm reel sayılardır. Bu fonksiyonun tanım kümesi üzerindeki her bir x elemanı için, f(x) değeri tektir. Bu nedenle, f(x) = 2x + 1 fonksiyonu tek değerlidir.

2. Soru: Tanım kümesi ve değer kümesi verilen bir fonksiyonun artıp azalıp azalmadığını nasıl anlarız?

Cevap: Bir fonksiyonun artıp azalıp azalmadığını anlamak için, fonksiyonun tanım kümesi üzerindeki iki x1 ve x2 elemanı için, x1 < x2 ise, f(x1) < f(x2) eşitliğinin her zaman sağlanıp sağlanmadığını kontrol etmemiz gerekir. Eğer fonksiyonun tanım kümesi üzerindeki her iki x1 ve x2 elemanı için, x1 < x2 ise, f(x1) < f(x2) eşitliği sağlanıyorsa, fonksiyon artandır. Eğer fonksiyonun tanım kümesi üzerindeki her iki x1 ve x2 elemanı için, x1 < x2 ise, f(x1) > f(x2) eşitliği sağlanıyorsa, fonksiyon azalandır.
Örneğin, f(x) = x^2 fonksiyonunun tanım kümesi, tüm reel sayılardır. Bu fonksiyonun tanım kümesi üzerindeki her iki x1 ve x2 elemanı için, x1 < x2 ise, f(x1) < f(x2) eşitliği sağlanmaktadır. Bu nedenle, f(x) = x^2 fonksiyonu artandır.