10. Sınıf Sayma Yöntemleri (Toplama ve Çarpma Yoluyla Sayma) Konu Anlatımı Matematik

Bire Bir Eşleme Yoluyla Sayma

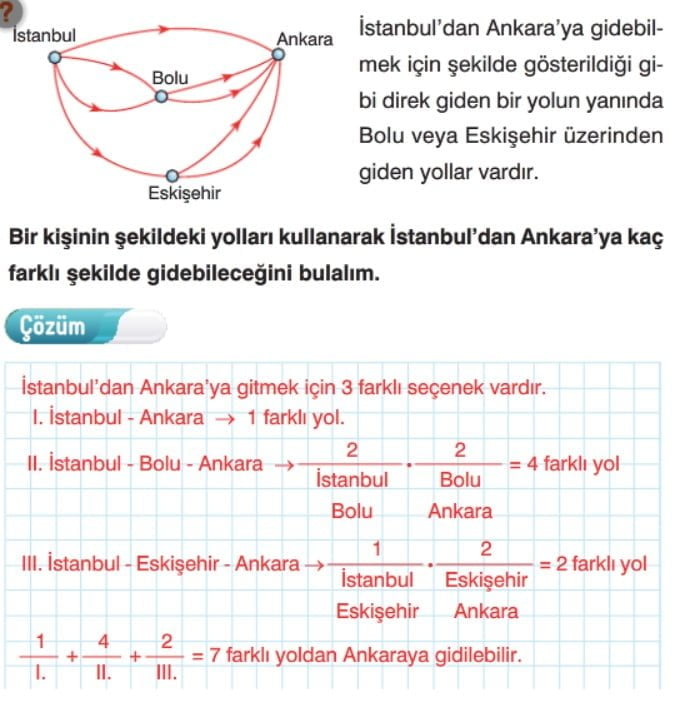
Toplama Yoluyla Sayma

Çarpma Yoluyla Sayma

Sayma Yöntemleri Çözümlü Sorular

Sayma Yöntemleri Video

1. Temel İlke: İkinci Kural (Çarpma Kuralı) Sayma yöntemlerinin temelinde "Çarpma Kuralı" bulunur. Bu kural, bir olayın gerçekleşme şekillerini sayma yöntemlerini kullanarak hesaplamamıza olanak tanır. İkinci Kural şu şekildedir:

• Eğer bir olayın ilk aşamasında m farklı şekilde gerçekleşebilir ve bu olayın ikinci aşamasında n farklı şekilde gerçekleşebilirse, bu iki aşamalı olayın toplam şekli m x n farklı şekilde gerçekleşir.

Örnek: Bir şifre, 4 haneli bir sayıdır ve her hanelerde 0-9 arası bir rakam kullanılabilir. Bu şifrenin kaç farklı şekilde oluşturulabileceğini bulalım.

• İlk hanelerde 10 farklı rakam kullanılabilir (0-9).
• İkinci hanelerde de 10 farklı rakam kullanılabilir.
• Üçüncü hanelerde de 10 farklı rakam kullanılabilir.
• Dördüncü hanelerde de yine 10 farklı rakam kullanılabilir.

Bu durumda, toplam farklı şifre sayısı: 10 x 10 x 10 x 10 = 10,000'dir.

2. Permütasyonlar ve Kombinasyonlar 10. sınıf seviyesinde, permütasyonlar (sıralı düzenlemeler) ve kombinasyonlar (sırasız düzenlemeler) gibi sayma yöntemlerini öğrenmeye başlarsınız. Permütasyonlar ve kombinasyonlar, nesnelerin sıralama ve seçim yöntemlerini inceleyen önemli konulardır.

• Permütasyon (nPr): n nesnenin sıralanma şekli nPr = n! / (n - r)!
• Kombinasyon (nCr): n nesnenin seçilme şekli nCr = n! / (r! * (n - r)!)

3. Muhtemel Problemler 10. sınıf seviyesinde, sayma yöntemleri sıklıkla muhtemel problemleri çözmek için kullanılır. Bu tür sorunlar, olasılık, olasılık dağılımları, rastgele değişkenler ve benzeri konuları içerebilir.

Örnek: Bir torbadan 4 farklı renkte top seçiyoruz. Bu 4 topu sırayla çekiyoruz. İlk çektiğimiz topun kırmızı olduğu ve sonra mavi, yeşil ve sarı topları çekeceğimiz bir olayın olasılığını hesaplayalım.

• İlk topu seçme şekli: 1 farklı renk seçimimiz var.
• İkinci topu seçme şekli: Geriye 3 farklı renk kaldı, bu yüzden 3 farklı renk seçimimiz var.
• Üçüncü topu seçme şekli: Geriye 2 farklı renk kaldı, bu yüzden 2 farklı renk seçimimiz var.
• Dördüncü topu seçme şekli: Geriye son renk kaldı, bu yüzden 1 farklı renk seçimimiz var.

Bu olayın toplam şekli: 1 x 3 x 2 x 1 = 6 farklı şekilde gerçekleşir.

Sonuç olarak, bu olayın olasılığı: 6 / (4 x 3 x 2 x 1) = 1/12'dir.

Sayma yöntemleri, daha karmaşık problemleri çözmek için temel bir araçtır ve matematik derslerinde ve olasılık problemlerini inceleyen konularda sıkça kullanılır. Bu temel bilgileri kavramak, daha ileri matematik konularında başarılı olmanıza yardımcı olacaktır.