10. Sınıf Tekrarlı Permütasyon Konu Anlatımı Matematik

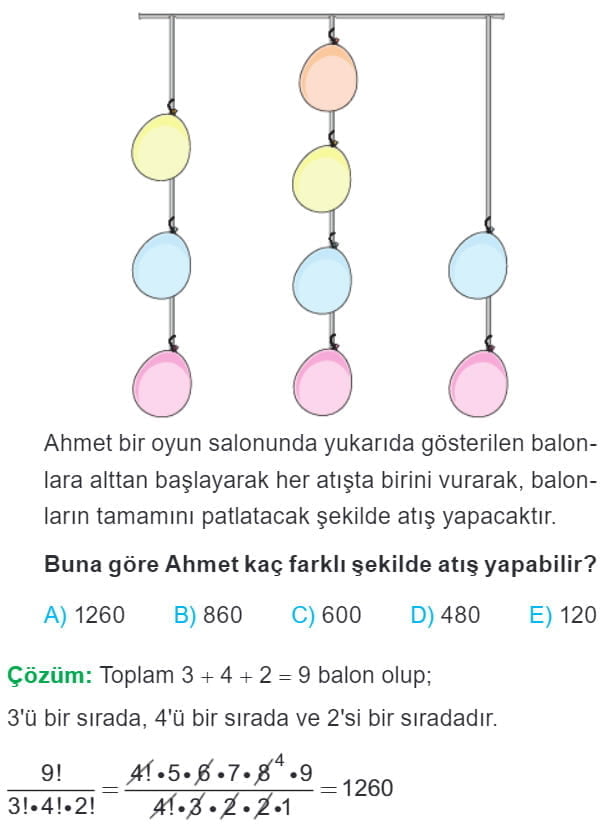
Tekrarlı Permütasyon Çözümlü Sorular

Tekrarlı Permütasyon Video

Tekrarlı permütasyon, matematikte sıralı düzenlemeleri ifade eden bir kavramdır. Bu konu, 10. sınıf öğrencileri için olasılık ve istatistik derslerinin bir parçası olarak öğretilir. Tekrarlı permütasyon, aynı öğe veya nesnelerin tekrar kullanılmasına izin verirken, nesnelerin sıralanma biçimlerinin sayısını hesaplamak için kullanılır. İşte tekrarlı permütasyon konusu hakkında temel bilgiler:

Tekrarlı Permütasyon Nedir? Tekrarlı permütasyon, nesnelerin sıralanma biçimlerini ifade eden bir kavramdır ve "n" nesnenin sıralanma biçimlerinin sayısını hesaplarken bazı nesnelerin tekrar kullanılmasına izin verir. Özellikle, nesneler sıralanırken bir nesnenin birkaç kez kullanılmasına olanak tanır.

Tekrarlı Permütasyon Notasyonu: Tekrarlı permütasyon genellikle "P(n, r)" ile gösterilir. Burada "n," toplam nesne sayısını ve "r," sıralamada her bir nesnenin tekrar sayısını temsil eder.

Tekrarlı Permütasyon Formülü: Tekrarlı permütasyon hesaplama için aşağıdaki formül kullanılır:
P(n, r) = n^r
Burada "n," toplam nesne sayısını temsil ederken, "r," her bir nesnenin tekrar sayısını ifade eder.
Tekrarlı Permütasyon Hesaplama Adımları: Tekrarlı permütasyon hesaplamak için aşağıdaki adımları izleyebilirsiniz:

• Toplam nesne sayısını (n) belirleyin.
• Her bir nesnenin kaç kez tekrarlandığını (r) belirleyin.
• Formülü kullanarak P(n, r) hesaplamasını yapın: P(n, r) = n^r.

Örnek: Bir çocuğun elinde 3 farklı renkte top var ve bu topları sıralayarak oynamak istiyor. Her rengi 2 kez kullanabilir. Kaç farklı sıralama biçimi vardır?
Çözüm: n = 3 (topların toplam sayısı) r = 2 (her rengi kullanma tekrarı)
P(3, 2) hesaplaması: P(3, 2) = 3^2 = 9
Sonuç olarak, çocuğun elindeki toplarla 9 farklı sıralama biçimi vardır.

Bu temel bilgiler ve formül, tekrarlı permütasyon konusunu anlamanıza yardımcı olacaktır. Daha karmaşık soruları çözerken bu temel kavramları kullanarak pratik yapabilirsiniz.

Soru: Bir şifre oluşturmak için 26 harf kullanılıyor. Bu harflerden 6 tanesini rastgele seçerek dizilişinin kaç farklı şekli olabilir?
Çözüm: Bu soruda, nesnelerin farklı olduğu bir permütasyon söz konusudur. Bu nedenle, nesnelerin yerleri değiştirildiği için farklı şekiller oluşur. Harflerin yerlerini rastgele seçeceğimiz için, her harf için 26 farklı seçenek vardır. Yani, harflerin dizilişinin kaç farklı şekli olabileceğini bulmak için, 26^6 sayısını hesaplamamız gerekir.
26^6 = 26 * 26 * 26 * 26 * 26 * 26 = 46656000
Cevap: 46656000

Soru: Bir kutuda 3 kırmızı, 2 mavi ve 1 yeşil top var. Bu toplardan 5 tanesini rastgele seçerek dizilişinin kaç farklı şekli olabilir?
Çözüm: Bu soruda, nesnelerin farklı olduğu bir permütasyon söz konusudur. Bu nedenle, nesnelerin yerleri değiştirildiği için farklı şekiller oluşur. Topların yerlerini rastgele seçeceğimiz için, her top için 5 farklı seçenek vardır. Yani, topların dizilişinin kaç farklı şekli olabileceğini bulmak için, 5^5 sayısını hesaplamamız gerekir.
5^5 = 5 * 5 * 5 * 5 * 5 = 3125
Cevap: 3125

Etkinlik 1: Renkli Boncuklar Malzemeler: Farklı renklerde boncuklar
Açıklama: Öğrencilere farklı renklerde 4 boncuk verin. Öğrencilere bu boncukları kullanarak kaç farklı sıralama yapabileceklerini hesaplamalarını söyleyin. Ardından, tekrarlı permütasyon formülünü kullanarak bu sorunun cevabını hesaplamalarını isteyin.

Etkinlik 2: Kitaplarınızı Sıralayın Malzemeler: Kitaplar (farklı sayıda kitap kullanabilirsiniz)
Açıklama: Öğrencilere farklı sayıda kitap verin ve bu kitapları sıralayarak kaç farklı sıralama biçimi elde edebileceklerini hesaplamalarını isteyin. Her öğrenci, kitapların sıralanma biçimlerini kağıda yazmalı ve sonrasında tekrarlı permütasyon formülünü kullanarak doğru cevabı hesaplamalıdır.

Etkinlik 3: Mektup Sıralamaları Malzemeler: Alfabe kartları (veya yazılı alfabe harf kartları)
Açıklama: Öğrencilere alfabe kartları verin ve bu kartları kullanarak kaç farklı 3 harfli kelime sıralayabileceklerini hesaplamalarını isteyin. Öğrenciler, her bir harfi sırayla seçerek farklı kelimeler oluşturmalı ve ardından tekrarlı permütasyon formülünü kullanarak doğru sayıyı hesaplamalıdır.