10. Sınıf Ters Fonksiyon Konu Anlatımı ve Çözümlü Sorular Matematik

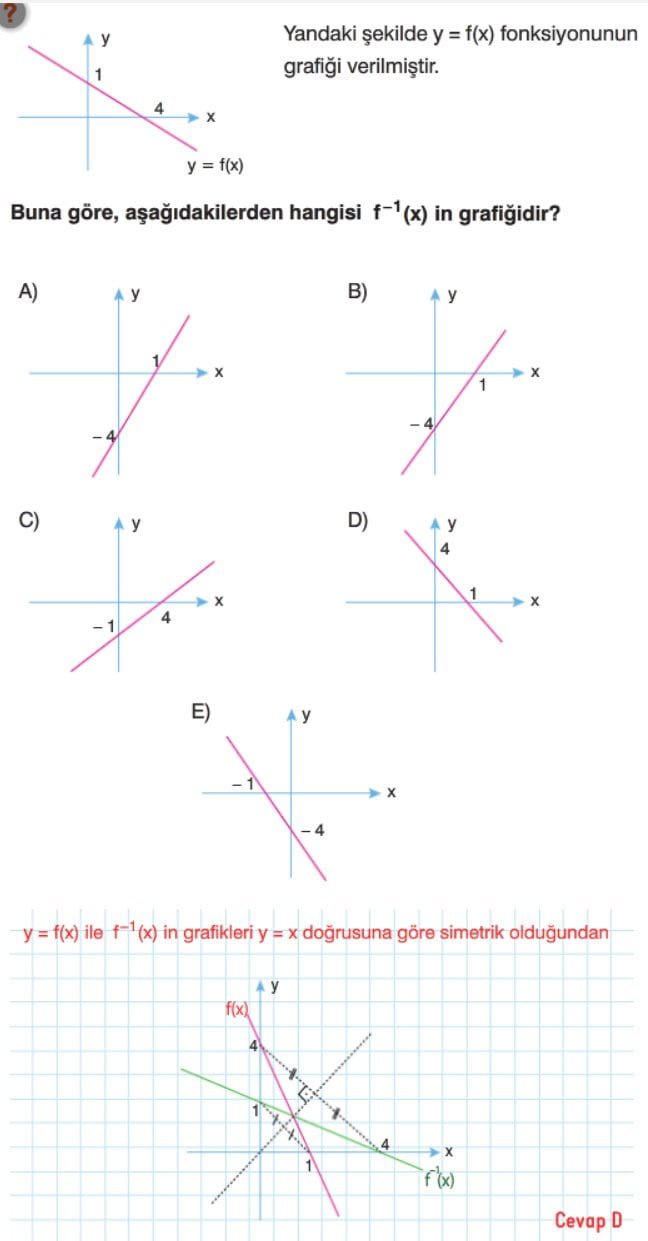
Bir Fonksiyonun Tersinin Grafiği

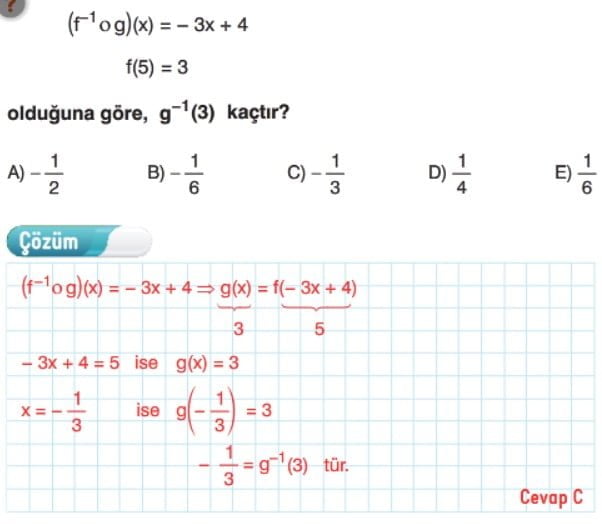
Ters Fonksiyon Çözümlü Sorular

Ters Fonksiyon Video

Ters Fonksiyonlar

Ters fonksiyon, bir fonksiyonun x değerine karşılık gelen y değerini veren fonksiyondur.

Ters fonksiyonlar, aşağıdaki şekilde tanımlanır:

f^-1(y) = x

Bu ifadede, f(x) bir fonksiyondur. f^-1(y) ifadesi, f(x) fonksiyonunun y değerine karşılık gelen x değerini verir.

Ters fonksiyonların bazı örnekleri şunlardır:

• f(x) = x^2 fonksiyonunun ters fonksiyonu, f^-1(y) = y^(1/2) fonksiyonudur.
• f(x) = 2x + 1 fonksiyonunun ters fonksiyonu, f^-1(y) = (y - 1)/2 fonksiyonudur.
• f(x) = ln(x) fonksiyonunun ters fonksiyonu, f^-1(y) = e^y fonksiyonudur.

Ters fonksiyonların özellikleri şunlardır:

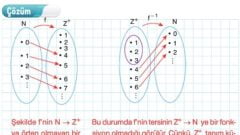
• Ters fonksiyonlar, her zaman bir fonksiyon değildir.
• Ters fonksiyonun varlığı için, fonksiyonun birebir ve örten olması gerekir.

Ters fonksiyonların bulunması, aşağıdaki adımları takip ederek yapılabilir:

1. Fonksiyonun birebir ve örten olup olmadığını kontrol edin.
2. Fonksiyonun birebir ve örten olduğunu tespit ederseniz, f(x) = y denklemi için x'i y'ye göre ifade edin.

Ters fonksiyonların uygulamaları şunlardır:

• Ters fonksiyonlar, matematiksel modelleme işlemlerinde kullanılır.
• Ters fonksiyonlar, istatistiksel analiz işlemlerinde kullanılır.
• Ters fonksiyonlar, bilgisayar bilimlerinde kullanılır.

Ters fonksiyonların özelliklerini anlamamız, bu fonksiyonların kullanıldığı alanlarda daha başarılı olmamızı sağlar.

Ters fonksiyon çözümlü sorular

1. Soru

f(x) = x^2 fonksiyonunun ters fonksiyonunu bulunuz.

Çözüm:

f(x) = y denklemi için x'i y'ye göre ifade ederiz.

x^2 = y

x = y^(1/2)

Cevap: f^-1(y) = y^(1/2)

2. Soru

f(x) = 2x + 1 fonksiyonunun ters fonksiyonunu bulunuz.

Çözüm:

f(x) = y denklemi için x'i y'ye göre ifade ederiz.

2x + 1 = y

x = (y - 1)/2

Cevap: f^-1(y) = (y - 1)/2

Bu soruların çözümleri, ters fonksiyonların temel özelliklerini anlamamıza yardımcı olur.

4. Soru

f(x) = x^3 fonksiyonunun ters fonksiyonunu bulunuz.

Çözüm:

f(x) = y denklemi için x'i y'ye göre ifade ederiz.

x^3 = y

x = y^(1/3)

Cevap: f^-1(y) = y^(1/3)

5. Soru

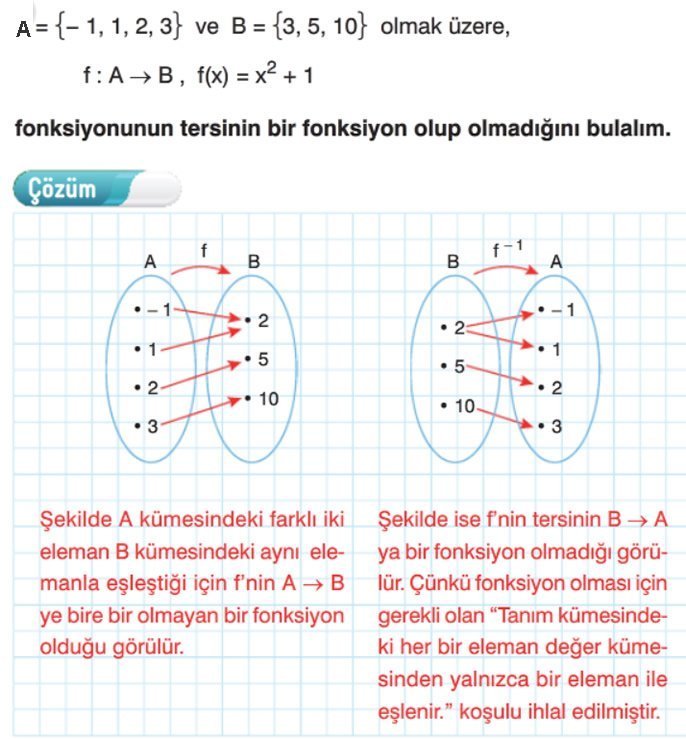
f(x) = x^2 + 1 fonksiyonunun ters fonksiyonunu bulunuz.

Çözüm:

f(x) = y denklemi için x'i y'ye göre ifade ederiz.

x^2 + 1 = y

x^2 = y - 1

x = y^(1/2) - 1

Cevap: f^-1(y) = y^(1/2) - 1

6. Soru

f(x) = |x| fonksiyonunun ters fonksiyonunu bulunuz.

Çözüm:

f(x) = y denklemi için x'i y'ye göre ifade edemeyiz.

Cevap: f^-1(y) fonksiyonu yoktur.