4, 5 ve 6 Basamaklı Doğal Sayılar Okunuşu ve Yazılışı – Bölük Kavramı – Çözümleme 4. Sınıf
Hatırlatma: Başında sıfır olmayan, üç rakamdan oluşan sayılara üç basamaklı doğal sayı denir. Bu sayılar, üç basamaktan oluşur ve en küçük üç basamaklı doğal sayı 100, en büyük ise 999’dur.
Dört Basamaklı Doğal Sayılar
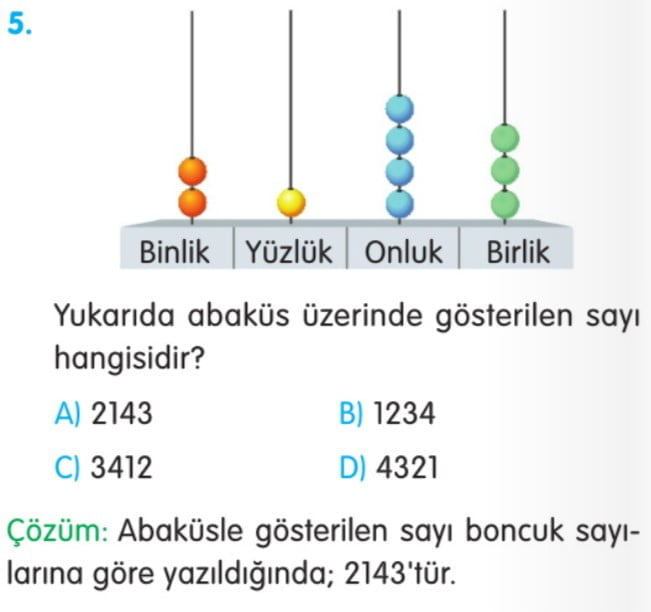
- Başta sıfır rakamı olmayan, dört rakamın yan yana gelerek oluşturduğu sayılara dört basamaklı doğal sayı denir. Bu sayılar, dört basamaktan oluşur ve en küçük dört basamaklı doğal sayı 1000, en büyük ise 9999’dur.
Dört basamaklı doğal sayılar, günlük hayatta birçok yerde karşımıza çıkar. İşte bazı örnekler:
- Para Miktarları: Büyük alışverişlerde veya maaş gibi ödemelerde dört basamaklı sayılar kullanılır. Örneğin, 2500 TL.
- Yıl İfadeleri: Tarihlerde yılı belirtmek için dört basamaklı sayılar kullanılır. Örneğin, 2024 yılı.
- Ev veya Apartman Numaraları: Bazı büyük binaların veya apartmanların numaraları dört basamaklı olabilir. Örneğin, 1024 numaralı daire.
- Ürün Fiyatları: Birçok ürünün fiyatı dört basamaklı olabilir. Örneğin, 1500 TL.
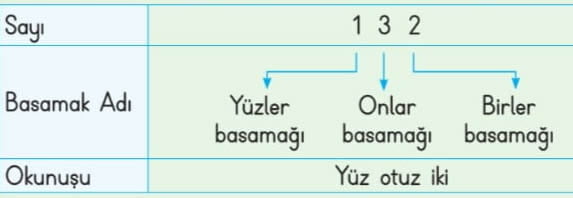
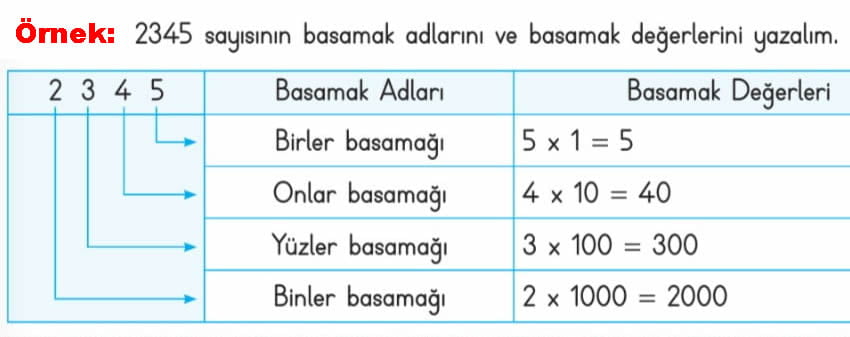
Basamak değeri: Bir sayının her bir rakamının bulunduğu basamağa göre sahip olduğu değerdir. Her rakamın değeri, o rakamın bulunduğu basamağa bağlı olarak değişir.
- Dört basamaklı doğal sayılar; birler, onlar, yüzler ve binler basamağından oluşur.
Örneğin, 4827 sayısını ele alalım:
- 4 binler basamağında yer alır ve 4000 değerindedir.
- 8 yüzler basamağında yer alır ve 800 değerindedir.
- 2 onlar basamağında yer alır ve 20 değerindedir.
- 7 birler basamağında yer alır ve 7 değerindedir.
Bu şekilde, her rakamın basamak değeri hesaplanarak sayının tam değeri bulunur.
Basamak değerleri toplam sayının kendisine eşittir.
Dört Basamaklı Doğal Sayıları Okuma ve Yazma
Dört basamaklı doğal sayılar, binler, yüzler, onlar ve birler basamağından oluşan sayılardır. Bu sayıları okurken, her basamaktaki rakam sırasıyla söylenir, sayının tamamı yazılırken ise rakamlar arka arkaya yazılır.
Örnekler:
- 4823 sayısı “dört bin sekiz yüz yirmi üç” olarak okunur.
- 2468 sayısı “iki bin dört yüz altmış sekiz” olarak okunur.
- 7314 sayısı “Yedi bin üç yüz on dört” olarak okunur.
- 1326 sayısı “Bin üç yüz yirmi altı” olarak okunur.
- 3057 sayısı “Üç bin elli yedi” olarak okunur.
- 3406 sayısı “Üç bin dört yüz altı” olarak okunur.
- 5790 sayısı “Beş bin yedi yüz doksan” olarak okunur.
Dört basamaklı doğal sayıları yazarken, binler, yüzler, onlar ve birler basamağındaki rakamları sırayla yazarız. Her basamaktaki rakamın bulunduğu yer, sayının değerini belirler.
Örnekler:
- Beş bin iki yüz otuz dört sayısını yazalım:
Binler basamağında 5, yüzler basamağında 2, onlar basamağında 3, birler basamağında 4 vardır.
Yazılışı: 5234 - Dokuz bin yedi sayısını yazalım:
Binler basamağında 9, yüzler basamağı 0 (yani yüzler basamağında sayı yok), onlar basamağında 0, birler basamağında 7 vardır.
Yazılışı: 9007 - Altı bin sekiz yüz sayısını yazalım:
Binler basamağında 6, yüzler basamağında 8, onlar basamağında 0, birler basamağında 0 vardır.
Yazılışı: 6800 - Beş bin yirmi sekiz sayısını yazalım:
Binler basamağında 5, yüzler basamağında 0, onlar basamağında 2, birler basamağında 8 vardır.
Yazılışı: 5028
Bu şekilde, verilen sayının söylenişine göre rakamları sırayla yazarak dört basamaklı doğal sayılar oluşturulur.
Doğal Sayılarda Bölük Kavramı ve Çözümleme
Dört basamaklı ve daha büyük sayılarda, sayının okunmasını ve yazılmasını kolaylaştırmak için sayı, üçer basamaklı gruplara ayrılır. Bu gruplara bölük denir. Her bölük, binler, milyonlar, milyarlar gibi adlarla anılır.
- Örneğin, 3254 sayısında:
3: Binler basamağındadır, binler bölüğündedir.
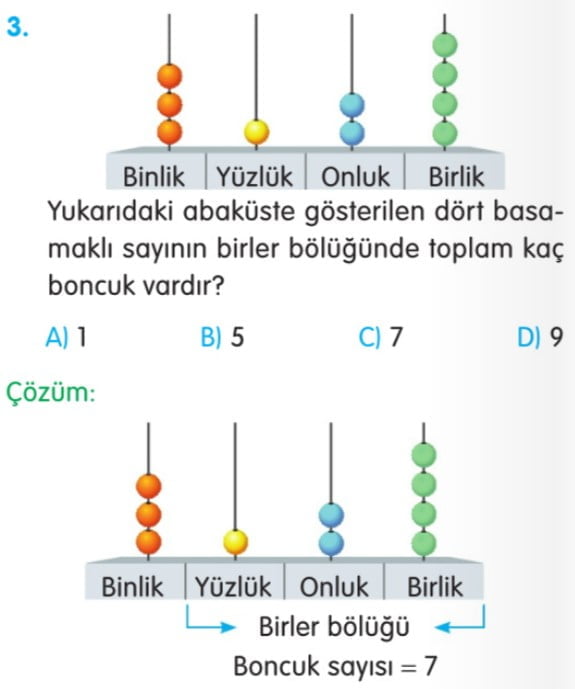
254: Yüzler, onlar ve birler basamaklarını içerir ve birler bölüğündedir. - Dört basamaklı sayıların birler bölüğünde birler, onlar, yüzler basamağı; binler bölüğünde ise binler basamağı vardır.
Çözümleme, bir sayıyı oluşturan basamaklardaki rakamların, kendi basamak değerleriyle çarpılarak elde edilen toplamı yazmaktır. Bu işlem, sayının hangi basamaklardan oluştuğunu ve her bir basamağın sayıya katkısını gösterir.
- Örnek: 3254 sayısını çözümleyelim:
3 binler basamağında yer alır ve değeri 3000‘dir.
2 yüzler basamağında yer alır ve değeri 200‘dür.
5 onlar basamağında yer alır ve değeri 50‘dir.
4 birler basamağında yer alır ve değeri 4‘tür.
Bu sayıyı çözümlediğimizde:
3254 = 3 x 1000 + 2 x 100 + 5 x 10 + 4 x 1
= 3000 + 200 + 50 + 4
= 3254 - Bu çözümlemede, her bir basamaktaki rakamın, o basamağın değerine karşılık gelen sayıyla çarpılarak toplamın elde edilmesi sağlanır.
Not: 0 (Sıfır)’ın bulunduğu basamak çözümlemede yazılmaz.
7405 = 7 x 1000 + 4 x 100 + 5 x 1
= 7000 + 400 + 5
= 7405

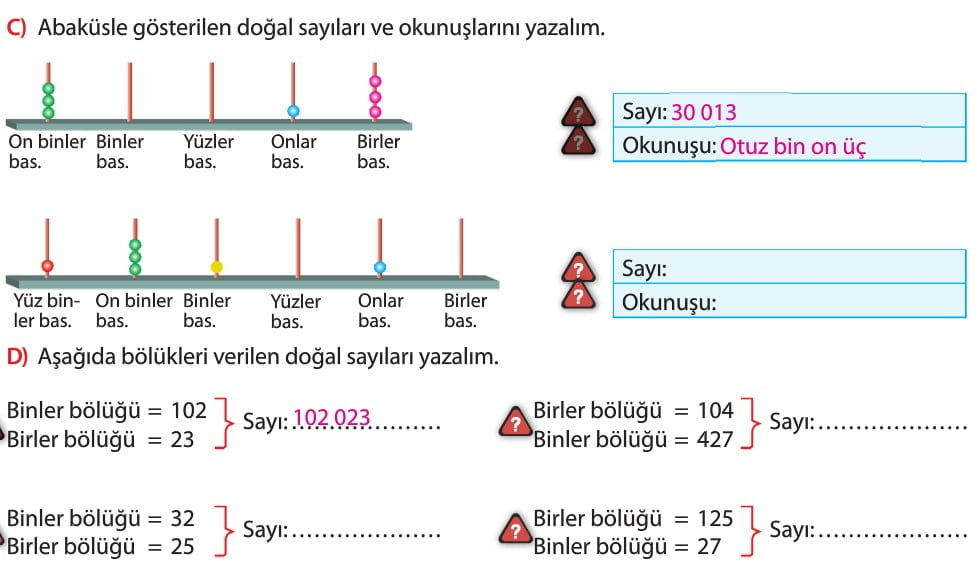
Beş Basamaklı Doğal Sayılar
- Başında sıfır olmayan beş rakamın yan yana gelerek oluşturduğu sayılara beş basamaklı doğal sayı denir.
- 5 basamaklı doğal sayıların birler bölüğünde birler, onlar, yüzler basamağı; binler bölüğünde ise binler ve on binler basamağı bulunur.
Beş Basamaklı Doğal Sayıları Okuma ve Yazma
- 5 basamaklı doğal sayıları okurken önce binler bölüğündeki iki basamaklı sayıyı okuyup “bin” deriz.
- Sonra kalan tüm sayıyı okuruz.
Örnek:
- 25 261: Yirmi beş bin iki yüz altmış bir
- 13 479: On üç bin dört yüz yetmiş dokuz
- 10 620: On bin altı yüz yirmi
- 99 009: Doksan dokuz bin dokuz
- Okunuşu verilen 5 basamaklı doğal sayıyı yazarken “bin” sözcüğünden önce gelen sayıyı yazarız.
- Sonra kalan sayıları yazarız.
Örnek:
- Otuz iki bin dokuz yüz on sekiz: 32 918
- Yetmiş bin altı yüz on: 70 610
- On iki bin beş yüz kırk üç: 12 543
- Kırk sekiz bin yirmi: 48 020
Örnek: Beş basamaklı 13 463 doğal sayısının bölüklerini, basamaklarını, basamak değerlerini, okunuşunu ve çözümlemesini gösterelim.
| Bölük Adları | Binler Bölüğü | Birler Bölüğü | |||
|---|---|---|---|---|---|
| Basamak Adları | On Binler Basamağı | Binler Basamağı | Yüzler Basamağı | Onlar Basamağı | Birler Basamağı |
| Sayı | 1 | 3 | 4 | 6 | 3 |
| Basamak Değeri | 10 000 | 3 000 | 400 | 60 | 3 |
| Sayının Okunuşu | On üç bin dört yüz altmış üç | ||||
| Çözümleme | 10 000 + 3 000 + 400 + 60 + 3 | ||||
13 463 sayısında:
Binler bölüğü: 13
Birler bölüğü: 463
Altı Basamaklı Doğal Sayılar
- Başında sıfır olmayan altı rakamın yan yana gelerek oluşturduğu sayılara altı basamaklı doğal sayı denir.
- 6 basamaklı doğal sayıların birler bölüğünde; birler, onlar, yüzler basamağı ve binler bölüğünde; binler, on binler ve yüz binler basamağı bulunur.
Altı Basamaklı Doğal Sayıları Okuma ve Yazma
- 6 basamaklı doğal sayılarda ilk olarak binler bölüğündeki üç basamaklı sayıyı okuyup “bin” deriz.
- Sonra kalan tüm sayıyı okuruz.
Örnek:
| Sayı | Okunuşu |
|---|---|
| 216 373 | İki yüz on altı bin üç yüz yetmiş üç |
| 909 320 | Dokuz yüz dokuz bin üç yüz yirmi |
| 812 003 | Sekiz yüz on iki bin üç |
| 100 500 | Yüz bin beş yüz |
- Okunuşu verilen 6 basamaklı doğal sayıyı yazarken “bin” sözcüğünden önce gelen sayıyı yazarız.
- Sonra kalan sayıları yazarız.
Örnek: Altı basamaklı 263 417 doğal sayısının basamak değerlerini tabloda gösterelim.
| Bölük Adları | Binler Bölüğü | Birler Bölüğü | ||||
|---|---|---|---|---|---|---|
| Basamak Adları | Yüz Binler Basamağı | On Binler Basamağı | Binler Basamağı | Yüzler Basamağı | Onlar Basamağı | Birler Basamağı |
| Sayı | 2 | 6 | 3 | 4 | 1 | 7 |
| Basamak Değeri | 200,000 | 60,000 | 3,000 | 400 | 10 | 7 |
| Sayının Okunuşu | İki yüz altmış üç bin dört yüz on yedi | |||||
| Çözümleme | 200,000 + 60,000 + 3,000 + 400 + 10 + 7 | |||||
263 417 sayısında:
Binler bölüğü: 263
Birler bölüğü: 417
4, 5 ve 6 Basamaklı Doğal Sayılar Etkinlikleri ve Çalışma Kağıdı
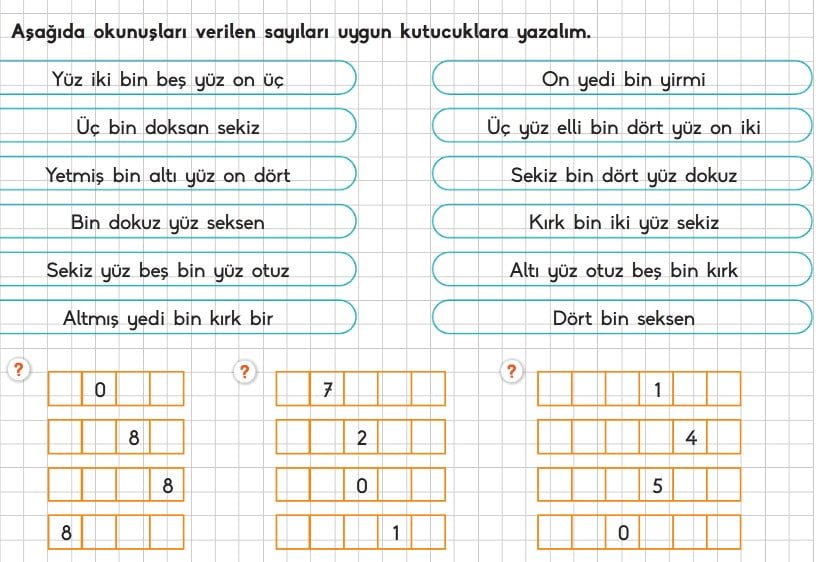
Aşağıdaki doğal sayıların okunuşlarını yazınız.
| Sayı | Okunuşu | Sayı | Okunuşu |
|---|---|---|---|
| 5432 | Beş bin dört yüz otuz iki | 123 978 | Yüz yirmi üç bin dokuz yüz yetmiş sekiz |
| 4321 | 860 120 | ||
| 1543 | 950 440 | ||
| 9748 | 517 301 | ||
| 43 405 | 556 510 | ||
| 16 180 | 210 199 | ||
| 80 761 | 987 610 | ||
| 43 422 | 203 540 |
Aşağıda okunuşları verilen doğal sayıları yazınız.
| Okunuş | Sayı | Okunuş | Sayı |
|---|---|---|---|
| Bin üç yüz iki | 1302 | Dokuz yüz yetmiş altı bin dokuz | 976 009 |
| Dört bin beş yüz on altı | Sekiz yüz seksen beş bin yedi | ||
| Beş bin elli beş | Dört yüz on iki bin üç | ||
| Sekiz bin dokuz | Yüz doksan bin beş yüz kırk iki | ||
| Dokuz bin yedi yüz iki | Sekiz yüz seksen bin | ||
| Kırk yedi bin sekiz | Yedi yüz elli altı bin dört | ||
| Otuz dört bin sekiz yüz on | Yüz elli dört bin otuz | ||
| Altmış üç bin beş yüz elli | Yüz yedi bin sekiz yüz altmış | ||
| Yetmiş yedi bin yedi | İki yüz doksan iki bin üç yüz on üç |
4, 5 ve 6 Basamaklı Doğal Sayılar Çözümlü Sorular
4, 5 ve 6 Basamaklı Doğal Sayılar Video
4. Sınıf 4, 5 ve 6 Basamaklı Doğal Sayılar Okunuşu ve Yazılışı, Bölük, Çözümleme
3. Sınıf öğrencileri için 4, 5 ve 6 basamaklı doğal sayılar konusu matematik öğreniminde önemli bir adımdır. Bu sayılar, temel aritmetik becerileri geliştirmek için kullanılır ve matematik konularının ilerleyen dönemlerinde de sık sık karşılarına çıkar. İşte 4, 5 ve 6 basamaklı doğal sayılar hakkında temel konu anlatımı:
4 Basamaklı Doğal Sayılar:
- 4 basamaklı doğal sayılar, 1000 ile 9999 arasındaki sayılardır.
- Örneğin, 3456 ve 7891 gibi sayılar 4 basamaklı doğal sayılardır.
- Bu sayıları okurken binler, yüzler, onlar ve birler basamaklarına dikkat edilir. Örneğin, 3456 sayısını "üç bin dört yüz elli altı" şeklinde okuyabilirsiniz.
5 Basamaklı Doğal Sayılar:
- 5 basamaklı doğal sayılar, 10,000 ile 99,999 arasındaki sayılardır.
- Örneğin, 12,345 ve 76,543 gibi sayılar 5 basamaklı doğal sayılardır.
- Sayıları okurken on binler, binler, yüzler, onlar ve birler basamaklarına dikkat edilir. Örneğin, 12,345 sayısını "on iki bin üç yüz kırk beş" şeklinde okuyabilirsiniz.
6 Basamaklı Doğal Sayılar:
- 6 basamaklı doğal sayılar, 100,000 ile 999,999 arasındaki sayılardır.
- Örneğin, 123,456 ve 987,654 gibi sayılar 6 basamaklı doğal sayılardır.
- Bu sayıları okurken yüz binler, on binler, binler, yüzler, onlar ve birler basamaklarına dikkat edilir. Örneğin, 123,456 sayısını "yüz yirmi üç bin dört yüz elli altı" şeklinde okuyabilirsiniz.
Bu basamaklı sayılarla ilgili temel aritmetik işlemler yapabilirsiniz. Toplama, çıkarma, çarpma ve bölme işlemlerini uygulayarak matematik becerilerinizi geliştirebilirsiniz. Bu konuyu anlamak için bolca pratik yapmanız önemlidir.
Bölük Nedir? Bölük, bir bölme işlemi sırasında bölenin içinde kaç tane sayı olduğunu veya bölenin kaç parçaya bölündüğünü ifade eder. Bölük, bölme işlemi sırasında bölme işleminin daha küçük adımlara ayrılmasını temsil eder. Öğrencilere, bölme işlemini daha basit adımlara bölmek ve bölmeyi daha kolay bir şekilde gerçekleştirmek için kullanılır.
Bir Örnek İle Bölük Kavramı: Öğrencilere, basit bir bölme işlemi üzerinden bölük kavramını açıklamak için bir örnek verilebilir. Örneğin, 28'i 4'e bölmeyi düşünelim. 28'i 4'e bölmek için adımları daha küçük parçalara ayırabiliriz:
- İlk olarak, 2'nin 4'e bölünmesini düşünelim. Ancak 2, 4'ten küçük olduğu için bu adımda bölüm tamamlanmaz.
- Daha sonra 28'in 4 ile bölünmesini düşünelim. Bu sefer 28, 4'e tam olarak bölünebilir. Yani, 4 bölük olarak kabul edilir. Bu bölüm sonucunda 4 bölük olarak kalır.
- Son olarak, 8'in 4'e bölünmesini düşünelim. 8 de 4'e tam olarak bölünebilir ve bu da 4 daha fazla bölük oluşturur.
Sonuç olarak, 28'i 4'e böldüğümüzde, 4 bölük olarak kabul edilir. Böylece, bölme işlemi sonucunda 28'in 4'e bölünmesi 7 olur. Bu, bölme işlemi sonucunda elde edilen kalan sayıdır.
4, 5 ve 6 Basamaklı Doğal Sayılar Etkinlikleri
Sayı Kartlarıyla Eşleştirme:
- Bu etkinlik için 4, 5 ve 6 basamaklı sayıları içeren kartlar hazırlayın.
- Öğrencilere bu kartları karıştırarak dağıtın ve her öğrenciye bir çift sayı kartı versin.
- Öğrencilere, kartları eşleştirmeleri ve her bir sayıyı doğru bir şekilde okumaları ve yazmaları gerektiğini söyleyin.
- Örneğin, bir öğrenci 4 basamaklı sayı olan "2,365" kartı ile "iki bin üç yüz altmış beş" kartını eşleştirmeye çalışsın.
Sayılarla Resim Yapma:
- Öğrencilere farklı sayılar kullanarak resimler çizmelerini isteyin. Örneğin, 4 basamaklı sayıları kullanarak bir dağ manzarası veya 5 basamaklı sayıları kullanarak bir ev çizmelerini isteyebilirsiniz.
- Öğrenciler resimlerini yaparken sayıların önemini anlayacaklar ve sayıları kullanarak farklı nesneler oluşturacaklardır.