6. Sınıf Asal Sayılar ve Doğal Sayıları Asal Çarpanlarına Ayırma Konu Anlatımı Matematik

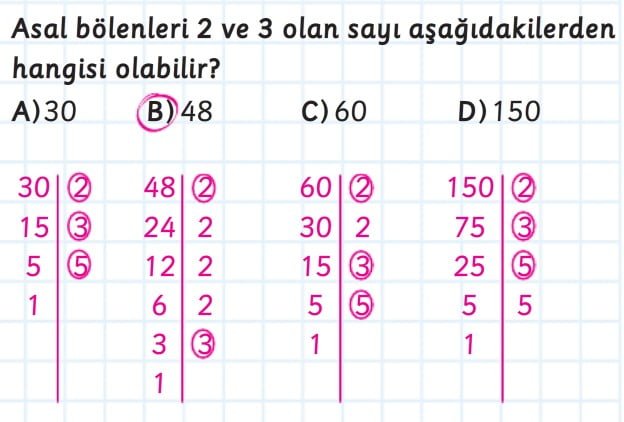
Asal Sayılar

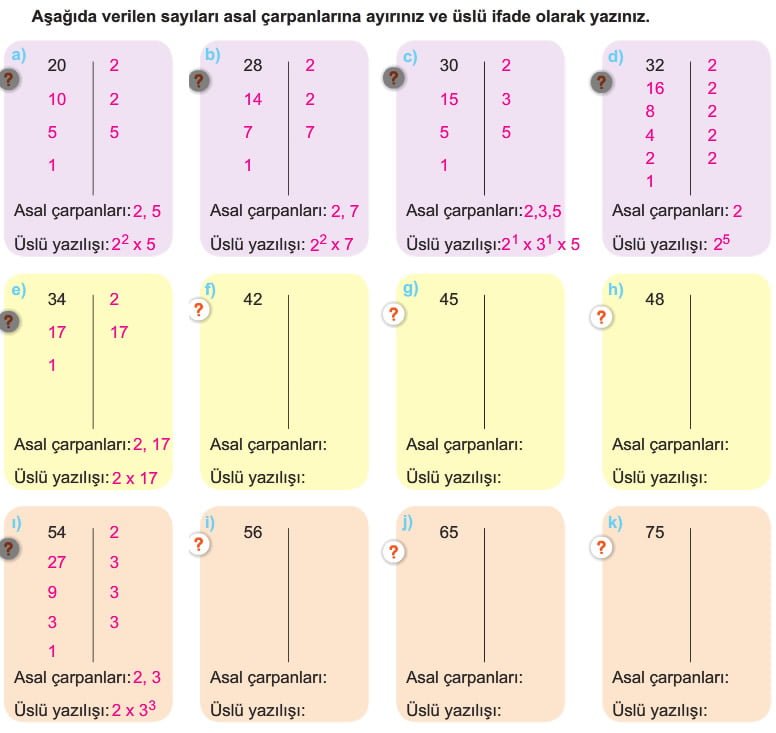
Doğal Sayıların Asal Çarpanları

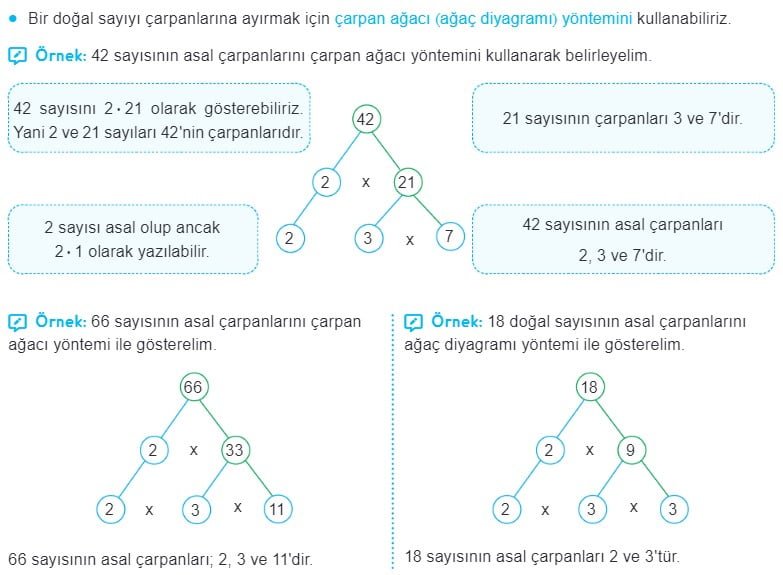
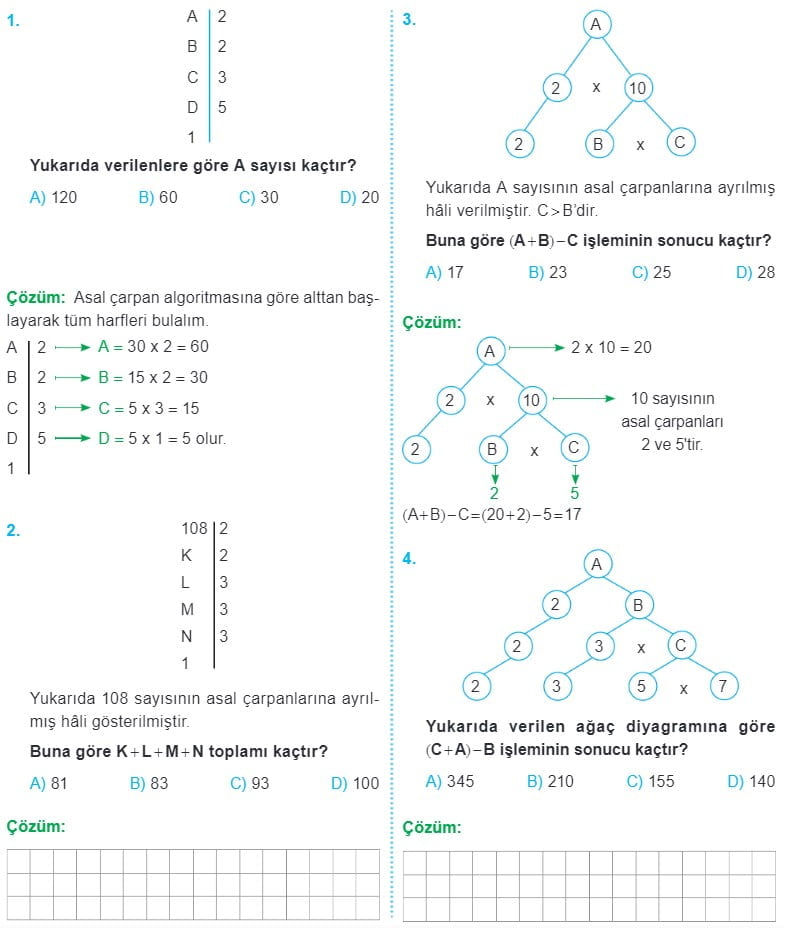
Asal Sayılar ve Doğal Sayıları Asal Çarpanlarına Ayırma Çözümlü Sorular

Asal Sayılar ve Doğal Sayıları Asal Çarpanlarına Ayırma Video

6. sınıf öğrencileri için asal sayılar ve doğal sayıları asal çarpanlarına ayırma konu anlatımı şu şekildedir:

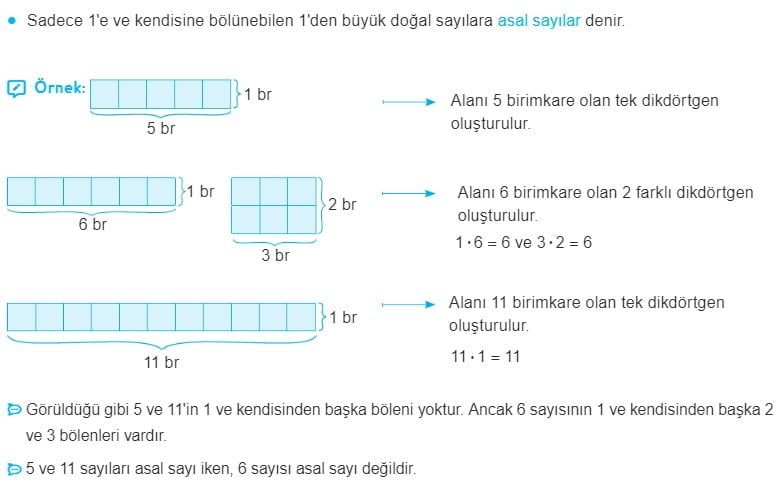
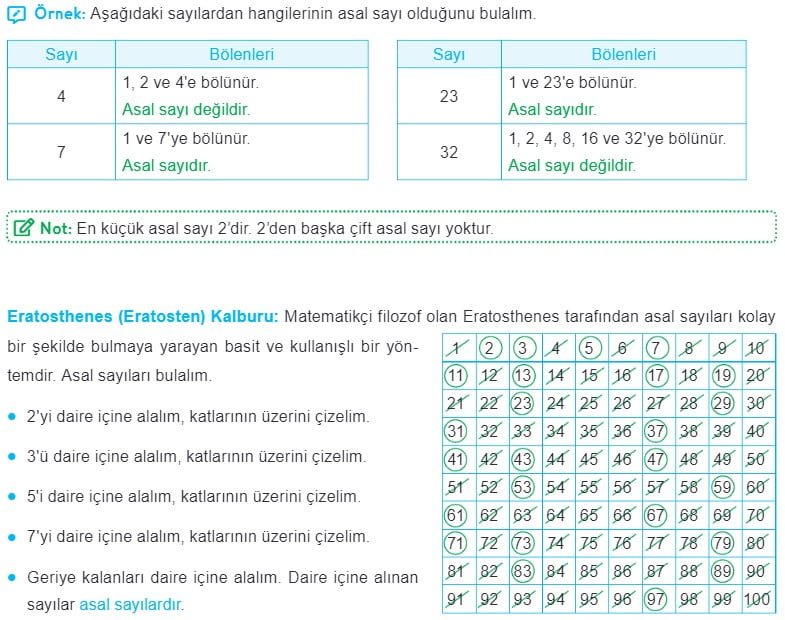
Asal Sayı Nedir?

• Asal sayılar, yalnızca 1 ve kendisi olmak üzere yalnızca iki pozitif çarpana sahip olan sayılardır. Örneğin, 2, 3, 5, 7, 11, 13, vb. asal sayılardır çünkü bu sayılar sadece 1 ve kendisi ile bölünebilirler.

Doğal Sayıları Asal Çarpanlarına Ayırma:

• Bir doğal sayıyı asal çarpanlarına ayırmak, o sayının çarpanlarını tespit etmek anlamına gelir. Her doğal sayı, bir veya daha fazla asal sayının çarpımı şeklinde ifade edilebilir.

Örnek 1: 36'yı Asal Çarpanlarına Ayırma:

• İlk adım, 36 sayısının çarpanlarını bulmaktır.
• 36, 2 ve 3 ile tam olarak bölünebilir, bu nedenle çarpanlar 2 ve 3'tür.
• 36 = 2 * 2 * 3 * 3
• Asal çarpanlarına ayırırsak: 36 = 2^2 * 3^2

Örnek 2: 48'i Asal Çarpanlarına Ayırma:

• İlk adım, 48 sayısının çarpanlarını bulmaktır.
• 48, 2, 3, ve 4 ile tam olarak bölünebilir, bu nedenle çarpanlar 2 ve 3'tür.
• Ancak, 4, 2'nin bir karesidir, bu nedenle ayrıca 2^2 olarak da ifade edilebilir.
• 48 = 2 * 2 * 2 * 2 * 3
• Asal çarpanlarına ayırırsak: 48 = 2^4 * 3

Örnek 3: 75'i Asal Çarpanlarına Ayırma:

• İlk adım, 75 sayısının çarpanlarını bulmaktır.
• 75, 3 ve 5 ile tam olarak bölünebilir, bu nedenle çarpanlar 3 ve 5'tir.
• 75 = 3 * 5 * 5
• Asal çarpanlarına ayırırsak: 75 = 3 * 5^2

Asal çarpanlarına ayırma, bir sayının farklı asal çarpanlarının çarpımı olarak ifade edilmesine yardımcı olur. Bu, matematiksel işlemleri daha kolay hale getirir ve sayıların özelliklerini daha iyi anlamamıza yardımcı olur. Ayrıca, bu yöntem sayıların faktöriyel ve bölenlerinin hesaplanmasında kullanılır.

Soru 1: 48 sayısını asal çarpanlarına ayırın.

Çözüm:

• 48'i asal çarpanlarına ayıralım:
• 48 = 2 * 24
• Şimdi 24'ü ayıralım:
• 24 = 2 * 12
• 12'yi ayıralım:
• 12 = 2 * 6
• 6'yı ayıralım:
• 6 = 2 * 3
• Şimdi her bir sayı asal bir çarpana sahip olduğundan sonuçları çarpalım:
• 48 = 2 * 2 * 2 * 2 * 3 = 2^4 * 3

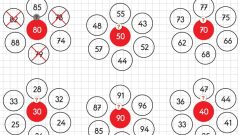
Soru 2: 90 sayısını asal çarpanlarına ayırın.

Çözüm:

• 90'ı asal çarpanlarına ayıralım:
• 90 = 2 * 45
• 45'i ayıralım:
• 45 = 3 * 15
• 15'i ayıralım:
• 15 = 3 * 5
• Şimdi her bir sayı asal bir çarpana sahip olduğundan sonuçları çarpalım:
• 90 = 2 * 3 * 3 * 5 = 2 * 3^2 * 5

Etkinlik 1: Asal Çarpan Bulmacası Öğrencilere farklı sayılar verin ve bu sayıları asal çarpanlarına ayırmalarını isteyin. Her öğrenci kendi sayısını sınıfta paylaşsın ve diğer öğrencilere sorusunu sorsun. Öğrenciler birbirlerinin sorularını çözsünler.

Etkinlik 2: Asal Çarpanlar Sıralama Öğrencilere rastgele birkaç sayı verin ve bu sayıların asal çarpanlarına ayırmalarını isteyin. Ardından, asal çarpanlarına ayrılmış bu sayıları sıralamalarını isteyin, böylece en küçükten en büyüğe doğru bir sıralama elde edilir.

Etkinlik 3: Asal Çarpan Bulma Yarışması Sınıfı iki gruba ayırın ve her iki gruba da farklı sayılar verin. Her grup, verilen sayıları asal çarpanlarına ayırmaya çalışsın. Hangi grup daha hızlı ve doğru bir şekilde sonuçları bulursa oyunu kazanır.