6. Sınıf Üslü İfadeler (Üslü Sayılar) Konu Anlatımı Matematik

6. Sınıf 6. Sınıf Matematik Konu Anlatımı Konu Anlatımı
11.10.2023

6. Sınıf Üslü İfadeler Konu Anlatımı

6. Sınıf Üslü İfadeler Çözümlü Sorular

6. Sınıf Üslü İfadeler Video

ETİKETLER:
BİR YORUM YAZIN

ZİYARETÇİ YORUMLARI - 0 YORUM

Henüz yorum yapılmamış.

6. Sınıf Üslü İfadeler Konu Anlatımı, Soru Çözümleri, Çalışma Kağıdı Örnekler

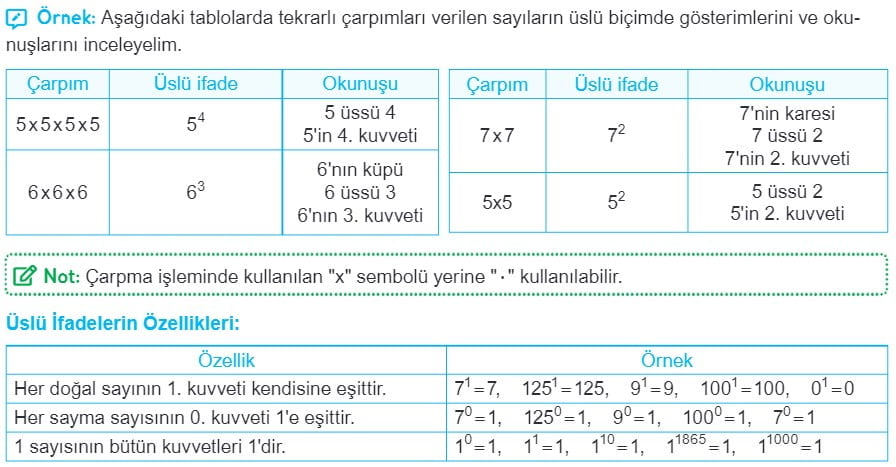
Üslü ifadeler, matematikte sayıları kuvvetli bir şekilde ifade etmek için kullanılan bir matematiksel notasyon veya semboldür. Üslü ifadeler, bir taban (base) ve bir üs (exponent) içerir. İşte 6. sınıf matematikte üslü ifadeler konusu hakkında temel bilgiler:

  • Üslü Sayının Yapısı: Bir üslü ifade, iki kısımdan oluşur:
    Taban (Base): Bu, kuvvetin alınan sayıdır. Yani, tabanın üzerine üs uygulanır.
    Üs (Exponent): Bu, tabanın kaç kez kendisiyle çarpılacağını belirler.
  • Üslü Sayının Okunuşu: "a üzeri n" şeklinde okunur ve "a" taban, "n" ise üs olarak okunur. Örneğin, 2 üzeri 3 (2^3), "iki üssü üç" şeklinde okunur.
  • Üslü İfadelerin Hesaplanması: Üslü ifadelerin değeri hesaplanırken, tabanın üs kadar kendisiyle çarpılması gerekmektedir. Örneğin, 2^3 = 2 x 2 x 2 = 8'dir.
  • Negatif Üsler: Eğer üs negatif bir sayı ise, sonuç ondalık bir kesirli sayı olacaktır. Örneğin, 2^(-2) = 1/4'dür.
  • Üs 0: Herhangi bir sayının üssü 0 ise sonuç her zaman 1'dir. Örneğin, 5^0 = 1'dir.
  • Üs 1: Herhangi bir sayının üssü 1 ise sonuç her zaman tabanın kendisiyle aynıdır. Örneğin, 7^1 = 7'dir.
  • Üslü İfadelerin İşlemleri: Üslü ifadeleri toplama, çıkarma, çarpma ve bölme işlemlerine tabi tutabilirsiniz. Aynı tabanlı üslü ifadeleri toplarken veya çıkarırken üsler aynı kalır, yani tabanlar aynı olmalıdır. Çarpma işleminde aynı tabanlı üslü ifadeleri toplarız. Bölme işleminde ise tabanlar farklı ise üsler aynı kalır.

Örnekler:
2^4 x 2^3 = 2^(4+3) = 2^7 = 128
(3^2)^3 = 3^(2x3) = 3^6 = 729
5^4 / 5^2 = 5^(4-2) = 5^2 = 25

Üslü ifadeler, matematiksel işlemlerde ve bilimsel hesaplamalarda sıklıkla kullanılır ve bu nedenle bu konunun iyi anlaşılması önemlidir.

Soru: 25 ifadesinin sonucunu hesaplayın.
Çözüm: 25 ifadesi, 2'nin 5. kuvvetini temsil eder. 2'nin 5. kuvveti, 2 x 2 x 2 x 2 x 2 olarak hesaplanır:
25 = 2 x 2 x 2 x 2 x 2 = 32
Yani, 25 ifadesinin sonucu 32'dir.

Soru: 34 / 32 ifadesinin sonucunu hesaplayın.
Çözüm: 34 / 32 ifadesi, 3'ün 4. kuvvetini 3'ün 2. kuvvetine bölmek anlamına gelir. Üssün çıkarma kuralını kullanarak bu işlemi yapabiliriz:
34 / 32 = 34-2 = 32
Şimdi, 32 ifadesinin sonucunu hesaplayabiliriz:
32 = 3 x 3 = 9
Yani, 34/ 32 ifadesinin sonucu 9'dur.