8. Sınıf En Büyük Ortak Bölen (EBOB) Konu Anlatımı Matematik

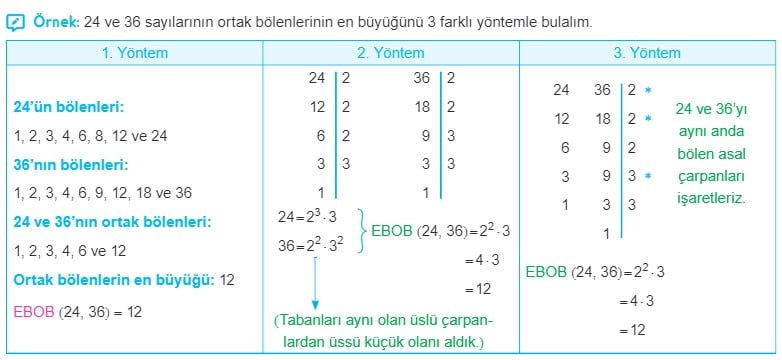
En Büyük Ortak Bölen (EBOB) Çözümlü Sorular

En Büyük Ortak Bölen (EBOB) Video

En Büyük Ortak Bölen (EBOB) Nedir?

En Büyük Ortak Bölen (EBOB), iki veya daha fazla sayının ortak bölenlerinin içinde en büyük olanıdır. EBOB, verilen sayıların en büyük bölenini bulmak için kullanılır. Genellikle "EBOB" veya İngilizce kısaltması olan "GCD" (Greatest Common Divisor) olarak ifade edilir.

EBOB, matematiksel işlemler, kümeler ve oranlar gibi birçok matematiksel konuda kullanılır. Aynı zamanda iki veya daha fazla kesirin sadeleştirilmesi veya oranlarının basitleştirilmesi için de önemlidir.

EBOB Nasıl Hesaplanır?

EBOB'u hesaplamak için genellikle iki yöntem kullanılır:

1. Çarpanları Kullanarak Yöntem: İki veya daha fazla sayının çarpanlarını belirleyin ve bu çarpanların ortaklarını bulun. Ortak çarpanlar arasından en büyük olanı EBOB'dur.
2. Algoritma Kullanarak Yöntem: İki sayı arasındaki EBOB'u hesaplamak için Euclid Algoritması gibi özel matematiksel algoritmalar kullanılabilir.

Çözümlü Soru 1: 18 ve 24 sayılarının EBOB'unu bulun.

Çözüm 1:

• İlk olarak, her iki sayının çarpanlarını listeleyelim.
  • 18'in çarpanları: 1, 2, 3, 6, 9, 18
  • 24'ün çarpanları: 1, 2, 3, 4, 6, 8, 12, 24
• Ortak çarpanlar: 1, 2, 3, 6
• En büyük ortak bölen (EBOB): 6

Çözümlü Soru 2: 15 ve 25 sayılarının EBOB'unu bulun.

Çözüm 2:

• İlk olarak, her iki sayının çarpanlarını listeleyelim.
  • 15'in çarpanları: 1, 3, 5, 15
  • 25'in çarpanları: 1, 5, 25
• Ortak çarpanlar: 1, 5
• En büyük ortak bölen (EBOB): 5

Çözümlü Soru 3: 36, 48 ve 60 sayılarının EBOB'unu bulun.

Çözüm 3:

• İlk olarak, her üç sayının çarpanlarını listeleyelim.
  • 36'nın çarpanları: 1, 2, 3, 4, 6, 9, 12, 18, 36
  • 48'in çarpanları: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
  • 60'ın çarpanları: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
• Ortak çarpanlar: 1, 2, 3, 4, 6, 12
• En büyük ortak bölen (EBOB): 12

Etkinlik 1: EBOB Bulma Yarışması

• Sınıfı öğrencileri gruplara ayırın.
• Her gruba rastgele iki veya daha fazla pozitif tam sayı verin.
• Her grup, verilen sayıların EBOB'unu bulmaya çalışsın.
• İlk EBOB'u bulan grup bir ödül kazansın.

Etkinlik 2: EBOB ve EKOK Karşılaştırması

• Öğrencilere rastgele iki sayı verin ve her iki sayının hem EBOB'unu hem de EKOK'unu hesaplamalarını isteyin.
• Sonuçları sınıfta paylaşarak hangi sayının daha büyük EBOB veya EKOK'a sahip olduğunu tartışın.
• Öğrencilere EBOB ve EKOK kavramlarının gerçek hayattaki kullanımını araştırmalarını isteyebilirsiniz.

Etkinlik 3: EBOB Bulma Oyunu

• Öğrencilere EBOB bulma oyunları oynatın. Örnek olarak, her iki öğrenciye bir çift sayı verin ve EBOB'u bulmalarını isteyin.
• Daha sonra öğrencileri rastgele gruplar oluşturarak bu oyunu sınıfta oynayın. Her turda yeni çiftler ve sayılar kullanabilirsiniz.

Problem 1: 24, 36 ve 48 sayılarının EBOB'unu bulun.

Problem 2: Bir çift ayakkabınızın numarası 10, diğer çiftin numarası 12. EBOB nedir?

Problem 3: Bir çocuk 24 elma, 30 muz ve 42 armut arasında eşit sayıda meyve almak istiyor. Hangi sayıda meyve almalıdır?

Problem 4: Bir çiftlikte 120 inek, 180 koyun ve 240 tavuk bulunmaktadır. Çiftlik sahibi, inekler, koyunlar ve tavuklar arasında aynı sayıda hayvanlarla yeni çiftlikler kurmak istiyor. Her yeni çiftlikte kaçar hayvan bulunmalıdır?