8. Sınıf İrrasyonel Sayılar ve Gerçek Sayılar Konu Anlatımı Matematik

İrrasyonel Sayılar ve Gerçek Sayılar Çözümlü Sorular

İrrasyonel Sayılar ve Gerçek Sayılar Video

İrrasyonel Sayılar:

İrrasyonel sayılar, ondalık kesirlerle tam olarak ifade edilemeyen sayılardır. Yani, irrasyonel sayılar kesirsiz bir ondalık gösterime sahiptirler, ancak bu ondalık gösterim sonsuz ve periyodik değildir. Örnek olarak √2, π (pi), ve e (Euler sayısı) gibi sayılar irrasyonel sayılardır.

Örneğin, √2'nin ondalık kesir gösterimi 1.414213562373095... şeklinde devam eder, ancak bir kesir olarak ifade edilemez.

Gerçek Sayılar:

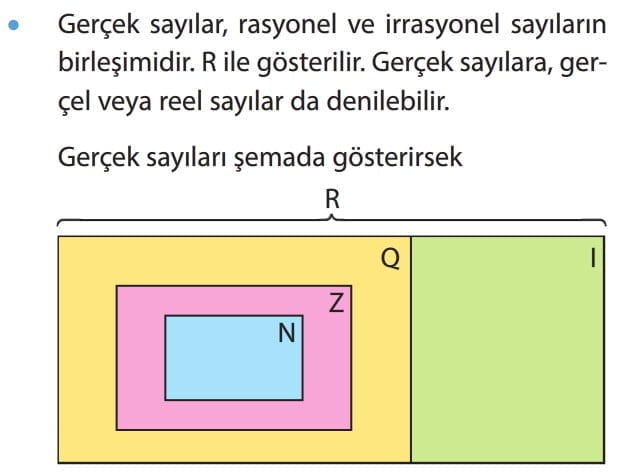
Gerçek sayılar, tüm rasyonel ve irrasyonel sayıları içeren bir sayı kümesidir. Bu nedenle gerçek sayılar, tam sayıları, kesirleri, ondalık sayıları, irrasyonel sayıları ve pozitif/negatif tüm sayıları içerir.

Gerçek sayılar, matematiksel işlemlerde ve problemlerde yaygın olarak kullanılır. Sayı çizgisi veya gerçek sayılar doğrusu, gerçek sayıları görsel olarak temsil etmek için kullanılır.

Örnekler:

• 3 (bir tam sayı) bir gerçek sayıdır.
• -2.5 (bir ondalık sayı) bir gerçek sayıdır.
• √5 (bir irrasyonel sayı) bir gerçek sayıdır.
• π (pi, bir irrasyonel sayı) bir gerçek sayıdır.
• 1/2 (bir kesir) bir gerçek sayıdır.

Gerçek sayılar, matematiksel analiz, cebir, geometri, ve diğer matematik branşlarında yaygın olarak kullanılır. İrrasyonel sayılar, geometri ve matematiksel problemlerde özellikle sıkça karşılaşılan önemli bir alt kümedir.

Çözümlü Soru 1: Verilen bir sayının irrasyonel mi yoksa rasyonel mi olduğunu belirleyin: √10

Çözüm 1: √10, bir irrasyonel sayıdır. Çünkü √10'un kesirli bir ondalık gösterimi yoktur, ve √10'nun ondalık ifadesi sonsuz bir desenle devam eder.

Çözümlü Soru 2: Aşağıdaki ifadelerden hangileri gerçek sayılardır, hangileri irrasyonel sayılardır?

a) -3.25 b) 0.5 c) √16 d) √7 e) π

Çözüm 2: a) -3.25: Gerçek sayı b) 0.5: Gerçek sayı c) √16: Gerçek sayı (çünkü √16 = 4) d) √7: İrrasyonel sayı e) π (pi): İrrasyonel sayı

Etkinlik Önerisi: İrrasyonel Sayıların Tanıtımı Öğrencilere farklı irrasyonel sayıları tanıtmak ve onları bulma pratiği yapmaları için bir etkinlik düzenleyin. Örneğin, √2, √5, ve √10'un ondalık gösterimlerini hesaplamalarını isteyebilirsiniz.

Etkinlik Önerisi: Sayı Çizgisi Oyunu Öğrencilere bir sayı çizgisi üzerinde gerçek ve irrasyonel sayıları işaretlemeleri için bir oyun düzenleyin. Her öğrenci sırayla bir sayı seçer ve bu sayıyı rasyonel veya irrasyonel olarak sınıflandırır. Doğru sınıflandırma yapan öğrencilere puan verin.