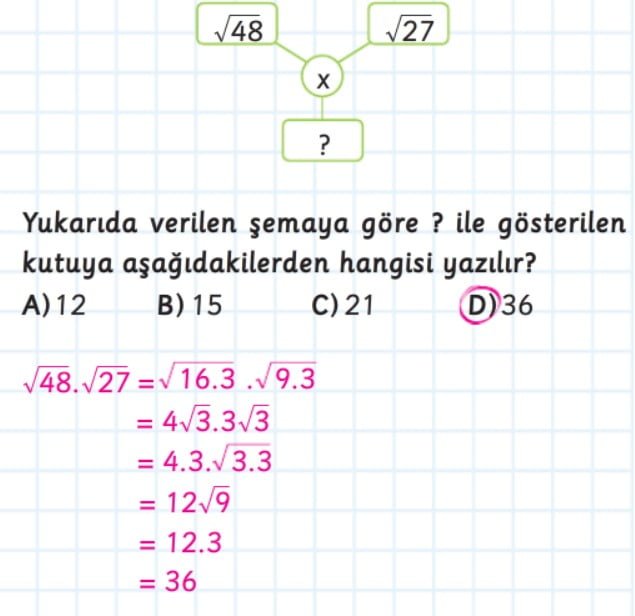
8. Sınıf Kareköklü İfadelerde Çarpma ve Bölme İşlemleri Konu Anlatımı Matematik

Kareköklü İfadelerde Çarpma İşlemi

Kareköklü İfadelerde Bölme İşlemi

Kareköklü İfadelerde Çarpma ve Bölme İşlemleri Çözümlü Sorular

Kareköklü İfadelerde Çarpma ve Bölme İşlemleri Video

Kareköklü İfadelerde Çarpma:

Kareköklü ifadelerde çarpma işlemi, iki kareköklü ifadeyi birleştirerek tek bir ifadeye dönüştürme işlemidir. İşte temel kurallar:

1. √a * √b = √(a * b): İki kareköklü ifadenin çarpımı, bu iki ifadenin çarpımının kareköküne eşittir. Bu, aynı radikand (alttaki sayı) sahip ifadeler için geçerlidir.

Örnek: √3 * √5 = √(3 * 5) = √15

2. √a * b = b * √a: Bir sayı ile karekök ifadesini çarparken, bu sayıyı radikandın önüne alabilirsiniz.

Örnek: 2 * √6 = √(2 * 6) = √12

Kareköklü İfadelerde Bölme:

Kareköklü ifadelerde bölme işlemi, iki kareköklü ifadeyi bölerek yeni bir ifade elde etme işlemidir. İşte temel kurallar:

1. (√a) / (√b) = √(a / b): İki kareköklü ifadesi bölünürse, bu iki ifadenin bölümünün karekökü elde edilir. Bu, aynı radikand sahip ifadeler için geçerlidir.

Örnek: (√12) / (√4) = √(12 / 4) = √3

2. (√a) / b = (√a) / b: Bir karekök ifadesini bir sayıya bölerken, karekök ifadesi aynen kalır, böldüğünüz sayı radikandın altına yazılır.

Örnek: (√15) / 5 = (√15) / 5

Kareköklü ifadelerde çarpma ve bölme işlemleri, matematiksel ifadeleri sadeleştirmek ve işlem yapmak için kullanılır. Bu kuralları anladığınızda, kareköklü ifadelerle daha karmaşık matematiksel problemleri çözebilirsiniz. Özellikle geometri ve trigonometri gibi konularda kareköklü ifadelerle sık sık karşılaşılır.

Çözümlü Soru 1: (√7) * (√3) ifadesini sadeleştirin.

Çözüm 1: (√7) * (√3) = √(7 * 3) = √21

Sonuç: (√7) * (√3) = √21

Çözümlü Soru 2: (√15) / (√5) ifadesini sadeleştirin.

Çözüm 2: (√15) / (√5) = √(15 / 5) = √3

Sonuç: (√15) / (√5) = √3

Etkinlik Önerisi: Çarpma ve Bölme Bulmacası Öğrencilere karmaşık kareköklü ifadeler içeren bir bulmaca hazırlayın. Öğrenciler, bu ifadeleri çarpma ve bölme işlemlerini kullanarak sadeleştirmeli veya sonuçlarını bulmalıdır. Doğru cevapları bulan öğrencilere puan verin.

Etkinlik Önerisi: Pratik Problemler Öğrencilere günlük yaşamda karşılaşılabilecek kareköklü ifadeler içeren pratik problemler verin. Örneğin, bir dikdörtgenin alanını hesaplamak veya bir üçgenin kenar uzunluğunu bulmak gibi problemler verilebilir. Öğrencilere bu problemleri çözme fırsatı verin ve sonuçları sınıfta tartışın.

Kareköklü ifadeler, matematikte önemli bir konsepttir ve özellikle geometri ve trigonometri gibi alanlarda sıkça karşılaşılır. Bu tür etkinlikler, öğrencilerin kareköklü ifadeleri sadeleştirme ve matematiksel problemlerde kullanma becerilerini geliştirmelerine yardımcı olabilir.