8. Sınıf Tam Sayıların Tam Sayı Kuvvetleri Konu Anlatımı Matematik

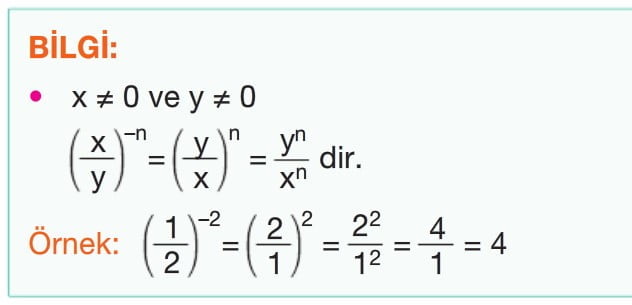
Tam Sayıların Tam Sayı Kuvvetleri Çözümlü Sorular

Tam Sayıların Tam Sayı Kuvvetleri Video

Tam Sayıların Tam Sayı Kuvvetleri: Tam sayıların tam sayı kuvvetleri, bir tam sayının kendisiyle çeşitli kuvvetlerle çarpılması sonucu elde edilen ifadelerdir. Bu kuvvetler pozitif tam sayılar olabileceği gibi negatif tam sayılar da olabilir.

• Pozitif Tam Sayı Kuvvetleri: Bir sayının pozitif tam sayı kuvvetleri, o sayının kendisi ile çeşitli pozitif tam sayılarla çarpılması sonucu elde edilen ifadelerdir. Örneğin, 2^3 (2'nin 3. kuvveti) = 2 x 2 x 2 = 8'dir.
• Negatif Tam Sayı Kuvvetleri: Bir sayının negatif tam sayı kuvvetleri, o sayının kendisi ile çeşitli negatif tam sayılarla bölünmesi sonucu elde edilen ifadelerdir. Örneğin, 2^(-2) (2'nin -2. kuvveti) = 1 / (2 x 2) = 1/4'dür.

Özel Durumlar:

• 0 Kuvveti: Herhangi bir sayının 0. kuvveti her zaman 1'dir. Örneğin, 5^0 = 1, 7^0 = 1 gibi.
• 1 Kuvveti: Herhangi bir sayının 1. kuvveti o sayının kendisine eşittir. Örneğin, 3^1 = 3, (-4)^1 = -4 gibi.

Çift ve Tek Kuvvetler:

• Pozitif çift tam sayı kuvvetleri, sonuç her zaman pozitif olur. Örneğin, (3^2) = 9, (-2^4) = 16 gibi.
• Pozitif tek tam sayı kuvvetleri, sayının işareti korunur. Örneğin, (-2^3) = -8, (4^5) = 1024 gibi.

Tam Sayı Kuvvetlerinin İşaret Değiştirmesi: Bir sayının negatif tam sayı kuvveti pozitif bir sonuç verir. Örneğin, (-2)^3 = -8'dir.

Bu kavramlar, matematik problemlerini çözmek ve sayıların kuvvetlerini anlamak için önemlidir. Öğrenciler, bu kavramları öğrenerek sayılarla ilgili daha karmaşık işlemleri çözebilirler.

Çözümlü Soru 1: 2^4 işleminin sonucunu hesaplayın.

Çözüm 1: 2^4, 2 x 2 x 2 x 2 = 16'dır.

Çözümlü Soru 2: (-3)^3 işleminin sonucunu hesaplayın.

Çözüm 2: (-3)^3, -3 x -3 x -3 = -27'dir.

Çözümlü Soru 3: 5^0 işleminin sonucu nedir?

Çözüm 3: Herhangi bir sayının 0. kuvveti her zaman 1'dir. Dolayısıyla, 5^0 = 1'dir.

Etkinlik 1: Kuvvetlerle Sayıları Karşılaştırma Oyunu Öğrencilere kuvvetlerle sayıları karşılaştırmaları için bir oyun hazırlayın. Örneğin, öğrencilere rastgele bir sayı veya kuvvet verin ve bu sayıyı veya kuvveti bir diğer öğrencinin verdiği sayı veya kuvvetle karşılaştırmalarını isteyin. Öğrenciler, hangi sayının veya kuvvetin daha büyük veya daha küçük olduğunu belirlemeye çalışacaklar.

Etkinlik 2: Kuvvetlerin Grafik İfadesi Öğrencilere farklı sayıların farklı kuvvetlerini hesaplamaları için bir görev verin. Ardından, bu hesaplamaları bir grafikle ifade etmelerini isteyin. Öğrenciler, x ekseni üzerinde sayıları, y ekseni üzerinde ise hesapladıkları kuvvetleri gösterebilirler. Bu grafiklerin nasıl göründüğünü ve hangi desenleri takip ettiğini inceleyebilirler.

Etkinlik 3: Bilinmeyen Kuvvetler Öğrencilere, belirli sayıların kuvvetlerini ifade eden denklemleri çözmeleri gereken problemler verin. Örneğin, "x^3 = 64" denklemini çözmelerini isteyebilirsiniz. Öğrenciler, bilinmeyen kuvvetin değerini hesaplamak için denklemin çözümünü bulmalıdır.