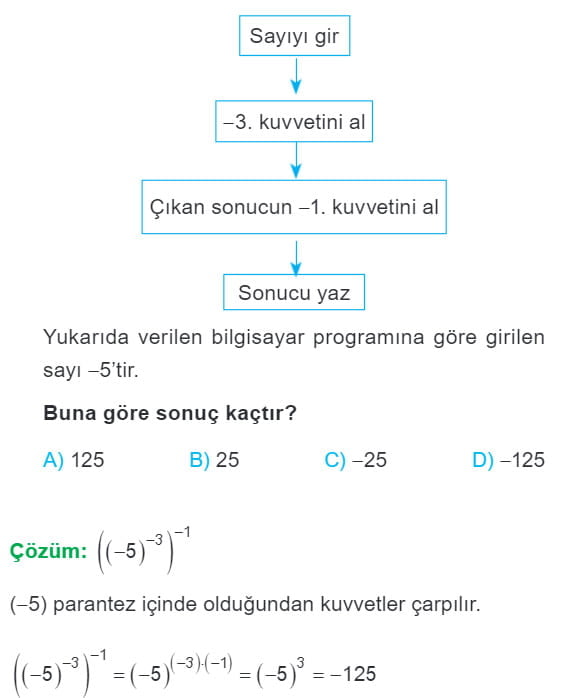
8. Sınıf Üslü İfadelerle İlgili Temel Kurallar Konu Anlatımı Matematik

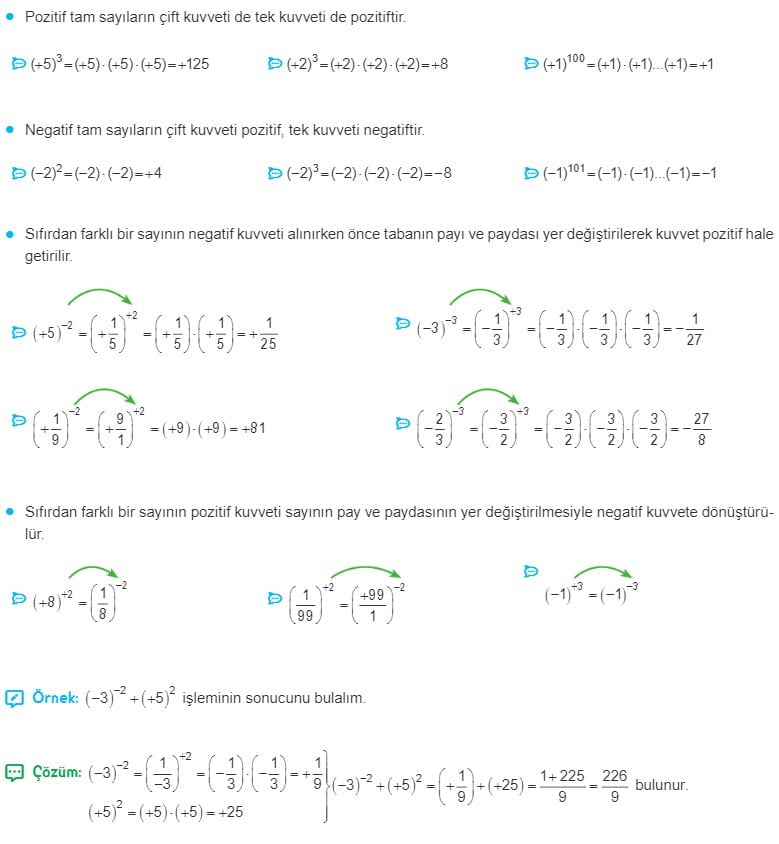
Üslü İfadelerle İlgili Temel Kurallar Çözümlü Sorular

Üslü İfadelerle İlgili Temel Kurallar Video

1. Üslerin Çarpılması: Aynı tabana sahip iki üslü ifade çarpıldığında, taban aynı kalmak kaydıyla üsler toplanır. Yani, a^(m) * a^(n) = a^(m+n).Örnek: 2^(3) * 2^(4) = 2^(3+4) = 2^(7) = 128.
2. Üslerin Bölünmesi: Aynı tabana sahip iki üslü ifade bölündüğünde, taban aynı kalmak kaydıyla üsler çıkarılır. Yani, (a^(m)) / (a^(n)) = a^(m-n).Örnek: 3^(5) / 3^(2) = 3^(5-2) = 3^(3) = 27.
3. Üssü 0 Olan Sayı: Herhangi bir sayının üssü 0 ise, sonuç her zaman 1'dir. Yani, a^(0) = 1.Örnek: 5^(0) = 1.
4. Üssü 1 Olan Sayı: Herhangi bir sayının üssü 1 ise, sonuç her zaman kendisi olur. Yani, a^(1) = a.Örnek: 7^(1) = 7.
5. Negatif Üsler: Bir sayının negatif bir üssü varsa, sonuç o sayının tersi olur. Yani, a^(-n) = 1 / (a^n).Örnek: 2^(-3) = 1 / (2^3) = 1 / 8.
6. Üssü Kesir Olan Sayılar: Bir sayının kesirli bir üssü varsa, kök işlemiyle ifade edilebilir. Yani, a^(m/n) = √(a^m) n'inci kökü.Örnek: 4^(1/2) = √(4) = 2.
7. Farklı Tabanlarla Çarpma ve Bölme: Farklı tabanlara sahip üslü ifadeleri çarpma veya bölme işlemleri direkt olarak gerçekleştirilemez, tabanlar aynı olmalıdır.Örnek (Geçersiz): 2^(3) * 3^(4) = 6^(7) (Çarpma işlemi doğru değil, tabanlar farklıdır).Örnek (Geçerli): (2^(3)) * (3^(4)) = 2^(3+4) * 3^(4) = 2^(7) * 3^(4).

Bu temel kurallar, üslü ifadelerin işlemesini ve sadeleştirilmesini daha anlaşılır hale getirir. Üslü ifadeler, matematiksel ifadeleri kısaltmak ve karmaşık işlemleri basitleştirmek için kullanılır. Bu nedenle, bu temel kuralları anlamak ve uygulamak matematikte önemlidir.

Çözümlü Soru 1: 2^3 * 2^5 ifadesinin sonucunu hesaplayın.

Çözüm 1: 2^3 * 2^5 = 2^(3+5) = 2^8 = 256.

Çözümlü Soru 2: (4^2) / (4^3) ifadesinin sonucunu hesaplayın.

Çözüm 2: (4^2) / (4^3) = 4^(2-3) = 4^(-1) = 1/4.

Çözümlü Soru 3: 3^4 * 3^(-2) ifadesinin sonucunu hesaplayın.

Çözüm 3: 3^4 * 3^(-2) = 3^(4-2) = 3^2 = 9.

Etkinlik Önerisi: Üslü İfadeler Bulmacası Öğrencilere bir üslü ifadeler bulmacası hazırlayın. Bulmacada, farklı tabanlar ve üslerle ilgili ifadeler verilir, ve öğrenciler bu ifadeleri sadeleştirmeli veya sonuçlarını hesaplamalıdır. Bu, öğrencilerin üslü ifadeleri kullanma becerilerini geliştirmelerine yardımcı olabilir.

Etkinlik Önerisi: Üslü İfadeler Quiz Öğrencilere üslü ifadelerle ilgili bir quiz hazırlayın. Quizde, öğrencilerin üslü ifadeleri değerlendirmeleri, işlemler yapmaları ve özel durumları anlamaları gerekebilir. Quiz sonuçları üzerinden tartışmalar yaparak eksiklikleri giderin.