9. Sınıf İki Kümenin Kartezyen Çarpımı Konu Anlatımı Matematik

Sıralı İkili

Kartezyen Çarpım Kümesi

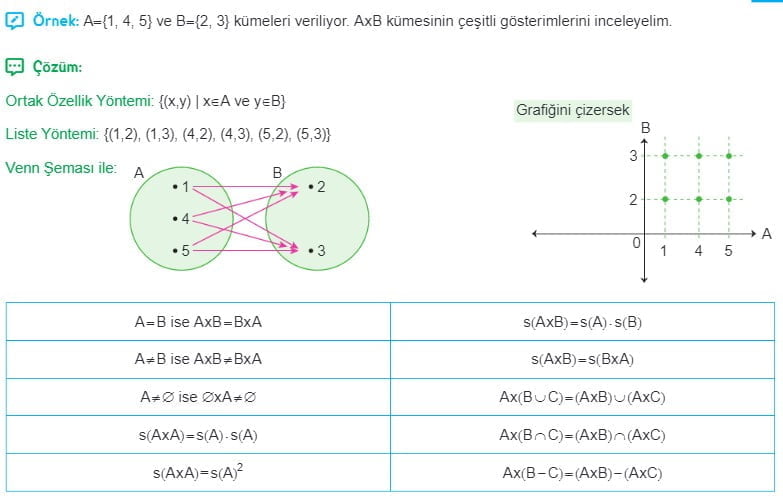
İki Kümenin Kartezyen Çarpımı Çözümlü Sorular

İki Kümenin Kartezyen Çarpımı Video

9. sınıf matematik dersinde, iki kümenin kartezyen çarpımı, özellikle cebir ve kümeler konularında önemli bir kavramdır. Kartezyen çarpım, iki farklı kümenin tüm olası sıralı çiftlerini oluşturan yeni bir kümedir. İki kümenin elemanlarının her bir kombinasyonunu içerir. İşte iki kümenin kartezyen çarpımı konusu hakkında daha fazla bilgi:

Kartezyen Çarpım Tanımı: Verilen iki küme A ve B'nin kartezyen çarpımı, A ile B'nin tüm olası sıralı çiftlerinin kümesidir ve A × B ile gösterilir. Matematiksel olarak şu şekilde ifade edilir:
A × B = {(a, b) | a ∈ A, b ∈ B}
Bu ifade, A kümesindeki her elemanı B kümesindeki her elemanla eşleştirir ve sıralı çiftler oluşturur. Bu nedenle kartezyen çarpım, sıralı çiftlerin bir kümesidir.

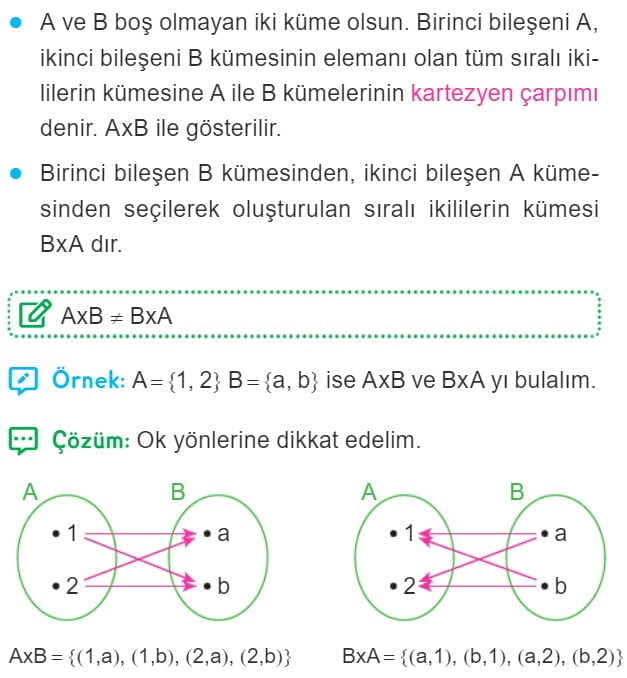
Örnek: A = {1, 2} B = {a, b, c}
A × B kartezyen çarpımını bulmak için her elemanı sırayla çapraz eşleştirelim:
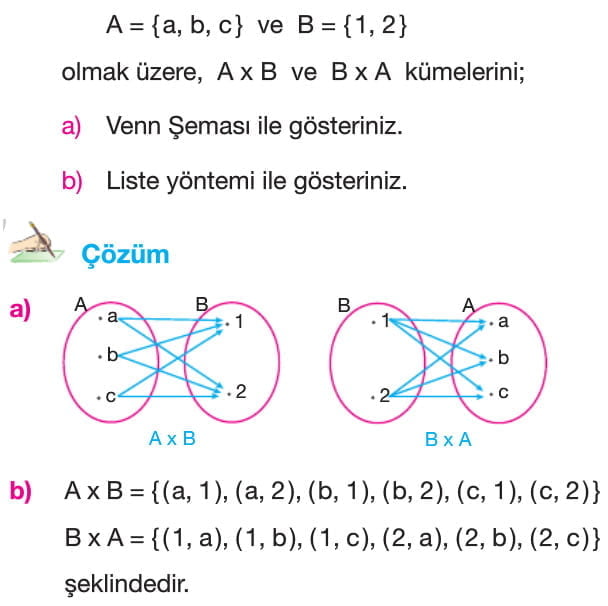
A × B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)}
Bu, A ve B kümesinin kartezyen çarpımını temsil eder. İki kümenin elemanlarının her birinin kombinasyonunu içerir.

Kartezyen çarpım, matematikte özellikle cebirsel yapıları, matrisleri ve sıralı verileri temsil etmek için yaygın olarak kullanılır. Bu nedenle bu konsepti iyi anlamak, daha ileri matematik konularını öğrenirken önemlidir.

Sıralı İkili (Sıralı Çift) Tanımı: Sıralı ikili veya sıralı çift, iki elemanın sıralı bir şekilde bir araya getirilmesiyle oluşan bir matematiksel yapıdır. Sıralı ikili, genellikle "(a, b)" şeklinde gösterilir, burada "a" ve "b" sırasıyla ilk ve ikinci elemandır. Sıralı ikili, elemanların sırasına dikkat eder, yani "(a, b)" ile "(b, a)" farklı sıralı ikililerdir.

Sıralı İkililerin Eşitliği: Sıralı ikililer, iki sıralı ikili arasında eşitlik ilişkisi kurulurken her iki elemanın da sırasının ve değerlerinin aynı olması gerektiği gibi kabul edilir. Yani iki sıralı ikili yalnızca elemanlarının değil, aynı zamanda sıralarının da aynı olması durumunda eşittir.

Örnek olarak, (3, 4) ve (4, 3) iki farklı sıralı ikilidir ve bu iki sıralı ikili birbirine eşit değildir. Ancak (3, 4) sıralı ikilisi kendisi ile eşittir.

Soru 1: Kartezyen Çarpım A = {1, 2} B = {a, b}

A ve B kümelerinin kartezyen çarpımını (A × B) bulun.

Çözüm 1: A × B = {(1, a), (1, b), (2, a), (2, b)}

Soru 2: Sıralı İkililerin Eşitliği Verilen sıralı ikililerden hangileri birbirine eşittir?

a) (3, 4) ve (4, 3) b) (2, a) ve (2, a) c) (1, b) ve (a, 1)

Çözüm 2: a) (3, 4) ve (4, 3) birbirine eşit değildir. b) (2, a) ve (2, a) birbirine eştir. c) (1, b) ve (a, 1) birbirine eşit değildir.

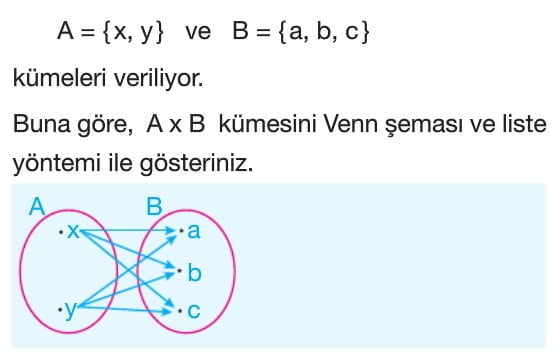
Etkinlik: Kartezyen Çarpım Bulmacası Öğrencilere A = {1, 2, 3} ve B = {x, y} gibi iki küme verin. Ardından, bu iki kümenin kartezyen çarpımını oluşturmalarını isteyin. Öğrenciler, tüm olası sıralı ikilileri yazmalıdır.

Soru 3: Kartezyen Çarpım ve Mantık İfadesi A = {1, 2, 3} B = {x, y, z}

A × B kartezyen çarpımını kullanarak, A kümesinin elemanlarından biri 2 ve B kümesinin elemanlarından biri z olan bir mantık ifadesi oluşturun.

Çözüm 3: A × B = {(1, x), (1, y), (1, z), (2, x), (2, y), (2, z), (3, x), (3, y), (3, z)}

Mantık ifadesi: "(2, z) ∈ A × B" (2 A kümesinin elemanıdır ve z B kümesinin elemanıdır.)