9. Sınıf İki Yönlü Koşullu Önerme (Ancak ve Ancak Bağlacı) Konu Anlatımı Matematik

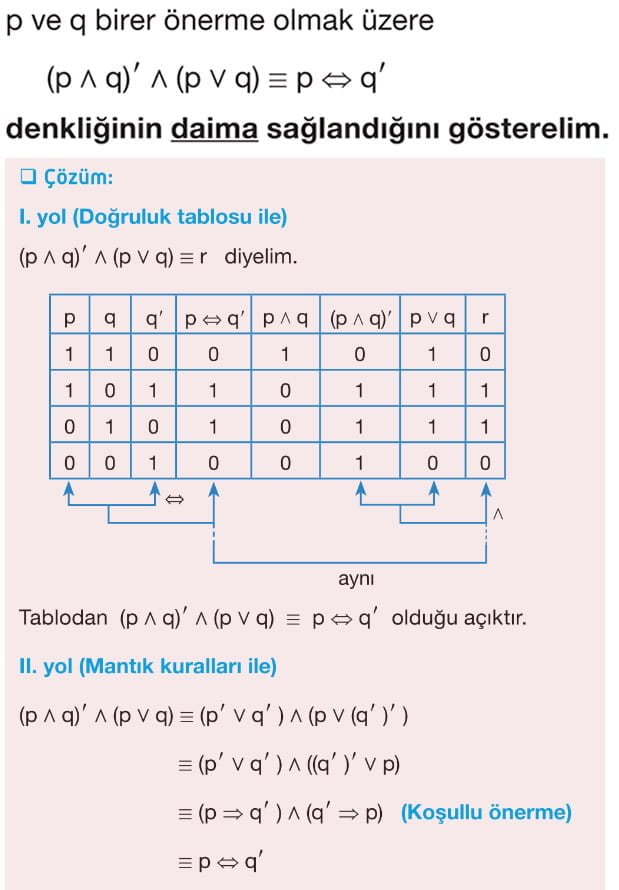
Ancak ve Ancak Bağlacının Özellikleri

Ancak ve Ancak Bağlacı Çözümlü Sorular

Ancak ve Ancak Bağlacı Video

9. sınıf matematikte, iki yönlü koşullu önerme (biconditional statement) veya "eşitlik" önermesi olarak adlandırılan bir tür önerme vardır. İki yönlü koşullu önerme, iki ifade arasındaki eşitlik veya denklik ilişkisini ifade eder. Genellikle "P if and only if Q" biçiminde temsil edilir ve "P ise ve yalnızca ise Q" veya "P ve Q eşittir" olarak okunur.

Örnek olarak, iki yönlü koşullu önermeyi şu şekilde ifade edebiliriz: "P: Bir üçgen bir eşkenar üçgense." "Q: Bir üçgenin tüm açıları eşittir."

İki yönlü koşullu önerme şu şekilde ifade edilir: "P if and only if Q" veya "P ⇔ Q"

Bu ifade, P ve Q arasında bir ilişki olduğunu ve iki ifadenin birbirine denk olduğunu belirtir. Yani, bir üçgen eşkenar üçgense, o üçgenin tüm açıları eşittir ve tersi de geçerlidir.

İki yönlü koşullu önermeler, matematikte ve mantıkta özellikle tanımlama ve denklik ilişkilerini açıklamak için kullanılır. Öğrencilere bu tür önermelerin anlamını ve kullanımını anlatmak, mantıklı düşünme yeteneklerini geliştirmelerine yardımcı olabilir.

Soru 1: İki Yönlü Koşullu Önerme Anlama P: "Bir çokgenin tüm iç açıları toplamı 180 derece." Q: "Bu çokgen bir üçgendir."

P ifadesi Q ifadesini gerektirir ve Q ifadesi P ifadesini gerektirir. İki yönlü koşullu önerme nedir?

Çözüm 1: İki yönlü koşullu önerme şu şekilde ifade edilir: "P if and only if Q" veya "P ⇔ Q." Bu ifade, bir çokgenin tüm iç açılarının toplamının 180 derece olması durumunda ve yalnızca bu durumda, bu çokgenin bir üçgen olduğunu ifade eder.

Soru 2: İki Yönlü Koşullu Önerme Oluşturma Öğrencilere farklı şekiller ve bu şekillerin özellikleri hakkında bilgi verin. Öğrencilere, bu şekillerin bir üçgen olup olmadığını ifade eden iki yönlü koşullu önermeler oluşturmalarını isteyin.

Örnek: Bir şeklin bir üçgen olduğunu ifade eden iki yönlü bir koşullu önerme yazın.

Soru 3: İki Yönlü Koşullu Önerme İspatı Öğrencilere, bir şeklin tüm iç açılarının toplamının 180 derece olması gerektiğini ve bu koşulun bir şeklin bir üçgen olduğu için gerekli ve yeterli bir koşul olduğunu belirten bir iki yönlü koşullu önerme verin. Ardından, bu önermenin doğruluğunu veya yanlışlığını ispat etmelerini isteyin.

9. sınıf matematikte, "ancak ve ancak" bağlacı, iki yönlü koşullu önermeleri ifade etmek için kullanılır. "Ancak ve ancak" ifadesi iki yönlü bir eşitlik veya denklik ilişkisini ifade eder ve iki ifade arasında karşılıklı bağımlılığı gösterir. İşte "ancak ve ancak" bağlacının özellikleri:

İki Yönlü Bağlantı: "Ancak ve ancak" ifadesi, iki ifadenin birbirine eşit olduğunu belirtir. Yani, her ikisi de birbirine bağlıdır ve biri doğru olduğunda diğeri de doğrudur.

İki Yönlü Koşul: Eğer iki önerme P ve Q arasında "ancak ve ancak" bağlacı kullanılıyorsa, bu ifade şu şekilde yazılabilir: "P ancak ve ancak Q." Bu ifade, hem P'nin Q'ya bağlı olduğunu hem de Q'nun P'ye bağlı olduğunu ifade eder.

Karşılıklı İlişki: "Ancak ve ancak" bağlacı, iki önerme arasında karşılıklı bir ilişkiyi gösterir. Yani, P doğruysa Q de doğru olur ve Q doğruysa P de doğru olur. Her iki önerme de birbirlerine bağlıdır.
Örnek: "Bir üçgen eşkenar üçgense, o üçgenin tüm açıları eşittir; ve bir üçgenin tüm açıları eşitse, o üçgen eşkenar üçgendir."

Bu ifade, "ancak ve ancak" bağlacını kullanarak iki yönlü bir eşitlik ilişkisi kurar. Bir üçgenin eşkenar olduğu ancak ve ancak tüm açılarının eşit olduğu durumlar geçerlidir.

Bu özelliklerle "ancak ve ancak" bağlacı, matematiksel ifadeleri veya mantıksal bağlantıları açıklamak ve analiz etmek için önemlidir. Bu bağlacın kullanımı, öğrencilere mantıklı düşünme ve mantıksal ilişkileri anlama becerisi kazandırabilir.

9. sınıf matematikte "çift gerektirme" veya "yalnızca gerektirme" mantık bağlacı, iki yönlü bir koşullu ifadeyi temsil eder. Bu bağlacı "ancak ve ancak" bağlacından ayıran önemli bir fark vardır. "Çift gerektirme," bir ifadenin diğer ifade için hem gerekli hem de yeterli olduğu bir ilişkiyi ifade eder. İşte "çift gerektirme"nin özellikleri ve kullanımı:

Çift Gerektirme İfadesi: "Çift gerektirme" ifadesi "P gerektirir Q ve Q gerektirir P" olarak ifade edilir. Bu ifade, P ve Q arasındaki karşılıklı ilişkiyi ifade eder. İki ifade arasında karşılıklı bağımlılık vardır.

Karşılıklı İlişki: "Çift gerektirme," iki ifade arasındaki karşılıklı bağımlılığı gösterir. P'nin doğru olabilmesi için Q'nun doğru olması gerekir ve aynı şekilde Q'nun doğru olabilmesi için P'nin doğru olması gerekir.

Örnek: "Bir sayı pozitif ve çiftse, o sayı 2'ye tam bölünebilir; ve bir sayı 2'ye tam bölünebilir ve pozitifse, o sayı çifttir."

Bu ifade, "çift gerektirme" bağlacını kullanarak iki ifade arasındaki karşılıklı bağımlılığı ifade eder. Bir sayının hem pozitif hem de çift olması gereklidir ve aynı zamanda 2'ye tam bölünebilmesi gerekir.

"Çift gerektirme" bağlacı, mantıksal düşünme ve matematiksel ifadeleri analiz etme becerilerini geliştirmek için önemlidir. Bu tür ifadeler, matematikte ve mantıkta kullanılırken dikkatli bir şekilde anlaşılmalıdır.