9. Sınıf Koşullu Önerme (İse Bağlacı – Karşıt, Tersi ve Karşıt Tersi) Konu Anlatımı Matematik

İse Bağlacının Özellikleri

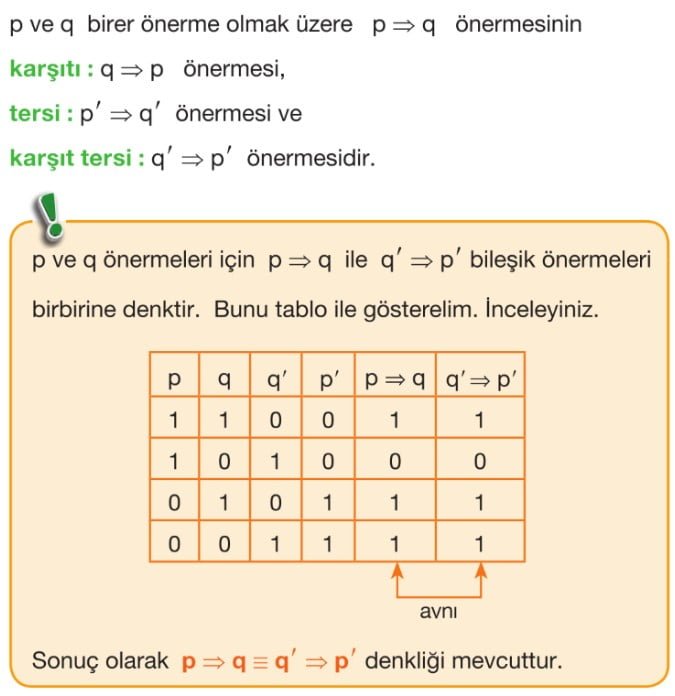
Koşullu Önermenin Karşıtı, Tersi, Karşıt Tersi

Koşullu Önerme (İse Bağlacı) Çözümlü Sorular

Koşullu Önerme (İse Bağlacı) Video

9. sınıf matematikte koşullu önermeler veya "ise" bağlacı ile ilgili bazı özellikleri şu şekilde açıklayabilirim:

Koşullu Önermenin Temsil Biçimi: Bir koşullu önerme, "P ise Q" biçiminde ifade edilir. "P" önkoşulu veya koşulu temsil ederken, "Q" sonucu temsil eder. Örnek: "Eğer hava güneşli ise, piknik yaparım."

Koşullu Önermenin Doğruluk Değerleri: Bir koşullu önermenin doğruluğu, koşulun doğru ve sonucun da doğru olduğu durumda gerçektir. Yani, P doğru ise ve Q doğruysa, koşullu önerme doğrudur. Ancak, P doğruyken Q yanlışsa, koşullu önerme yanlıştır. Koşul yanlışsa, sonucun doğru ya da yanlış olması durumlarına bağlı olarak, koşullu önerme doğru veya yanlış olabilir.

Karşıt ve Tersi: Bir koşullu önermenin karşıtı, koşulun doğru olduğu durumda sonucun yanlış olduğu bir ifadedir. Koşullu önermenin tersi, koşulun yanlış olduğu durumda sonucun yanlış olduğu bir ifadedir. Koşullu önermenin karşıtı ve tersi, koşullu önermenin doğru olduğu durumları temsil eder.

Özel Durumlar ve İstisnalar: Koşullu önermeler, özel durumları ve istisnaları ifade etmek için kullanılır. Özellikle matematiksel çıkarımlar ve mantık problemleri çözülürken önemlidirler.

Öğrenciler, koşullu önermelerin bu özelliklerini anlayarak mantıklı düşünme ve problem çözme yeteneklerini geliştirebilirler. Bu konsept, matematik, mantık ve bilgisayar bilimlerinde önemli bir rol oynar.

Koşullu Önermenin Karşıtı: Koşullu bir önermenin karşıtı, koşulun doğru olduğu, ancak sonucun yanlış olduğu bir ifadedir. Bir koşullu önerme "P → Q" ise, koşullu önermenin karşıtı "P → ¬Q" şeklinde ifade edilir. Bu, koşulun doğru olduğu durumda sonucun yanlış olduğunu ifade eder.

Örnek: "Eğer hava güneşli ise, dışarıya pikniğe giderim." Koşullu önermenin karşıtı, "Eğer hava güneşli ise, dışarıya pikniğe gitmem."

Koşullu Önermenin Tersi: Koşullu bir önermenin tersi, koşulun yanlış olduğu, sonucun da yanlış olduğu bir ifadedir. Bir koşullu önerme "P → Q" ise, koşullu önermenin tersi "¬P → ¬Q" şeklinde ifade edilir. Bu, koşulun yanlış olduğu durumda sonucun da yanlış olduğunu ifade eder.
Örnek: "Eğer hava yağmurlu ise, parka gitmem." Koşullu önermenin tersi, "Eğer hava yağmurlu değilse, parka giderim."

Koşullu Önermenin Karşıt Tersi: Koşullu bir önermenin karşıt tersi, koşulun yanlış olduğu, ancak sonucun doğru olduğu bir ifadedir. Bir koşullu önerme "P → Q" ise, koşullu önermenin karşıt tersi "¬Q → ¬P" şeklinde ifade edilir. Bu, sonucun doğru olduğu durumda koşulun yanlış olduğunu ifade eder.
Örnek: "Eğer sınavı geçersen, ödül alırsın." Koşullu önermenin karşıt tersi, "Eğer ödül almadıysan, sınavı geçmedin."
Bu özellikler, koşullu önermelerin analizi ve mantıksal düşünme becerilerinin geliştirilmesi açısından önemlidir. İlgili problemleri çözerken bu tür özelliklerin anlaşılması matematiksel mantık ve çıkarım yapma yeteneğini geliştirebilir.

Soru 1: Koşullu Önermeleri Anlama P: "Hava güneşli ise, dışarıya giderim." Q: "Dışarıya gittim."

Eğer P doğru ve Q yanlışsa, bu koşullu önerme doğru mu yanlış mıdır?

Çözüm 1: Koşullu önerme P → Q ifadesi, P doğru ve Q yanlış olduğunda yanlış olur. Bu nedenle, koşullu önerme yanlıştır.

Soru 2: Koşullu Önermeleri Oluşturma Öğrencilere farklı senaryolar verin ve bu senaryolardan koşullu önermeler oluşturmalarını isteyin. Örnek senaryolar şunlar olabilir:

• Senaryo 1: "Eğer yağmurlu bir günse, evde kalırım."
• Senaryo 2: "Eğer dersi geçersem, ödül alırım."

Öğrenciler, verilen senaryoları kullanarak koşullu önermeleri yazmalıdırlar.

Soru 3: Mantıksal Bağlaçlar ve Çıkarımlar Öğrencilere farklı koşullu önermeler ve sonuç önermeleri verin ve bu önermeleri kullanarak mantıklı çıkarımlar yapmalarını isteyin. Öğrencilerden, bir koşulun doğru olduğunda sonucun ne olduğunu tahmin etmelerini ve bu çıkarımları yazmalarını isteyin.

Örnek: Koşullu Önerme: "Eğer sınavı geçersen, ödül alırsın." Sonuç Önermesi: "Ödül aldım." Çıkarım: "Sınavı geçtim, çünkü ödül aldım."

Bu tür sorular ve etkinlikler, öğrencilerin mantıklı düşünme yeteneklerini geliştirmelerine yardımcı olabilir ve koşullu önermelerin doğru değerlendirilmesini sağlar.