9. Sınıf Kümelerde İşlemler Konu Anlatımı Matematik

Kümelerde Birleşim İşlemi

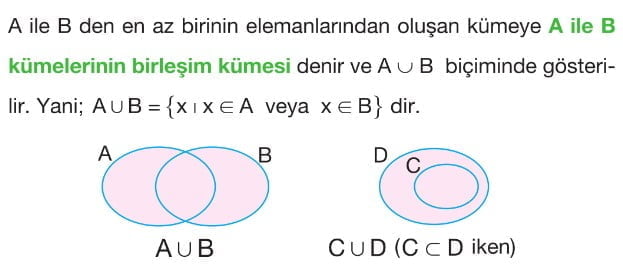
Kümelerde Birleşim İşleminin Özellikleri

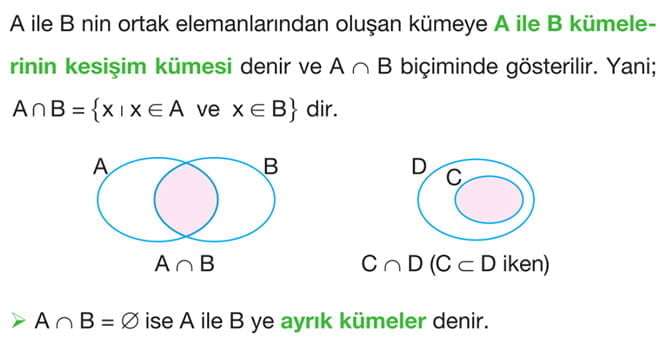
Kümelerde Kesişim İşlemi

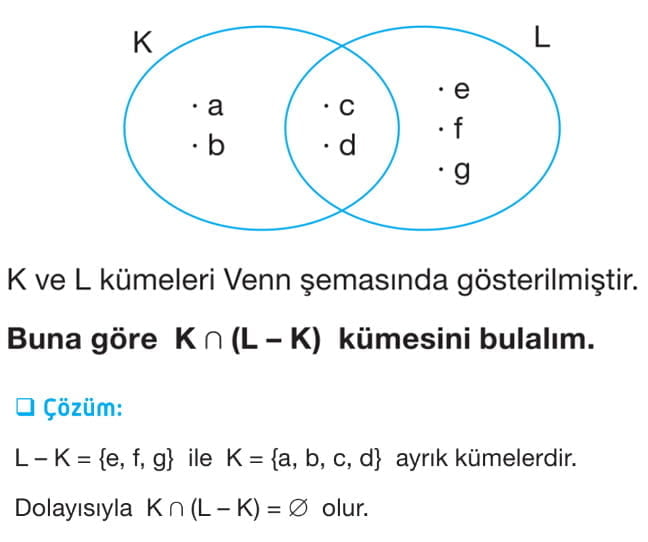
Örnek:

Kümelerde Kesişim İşleminin Özellikleri

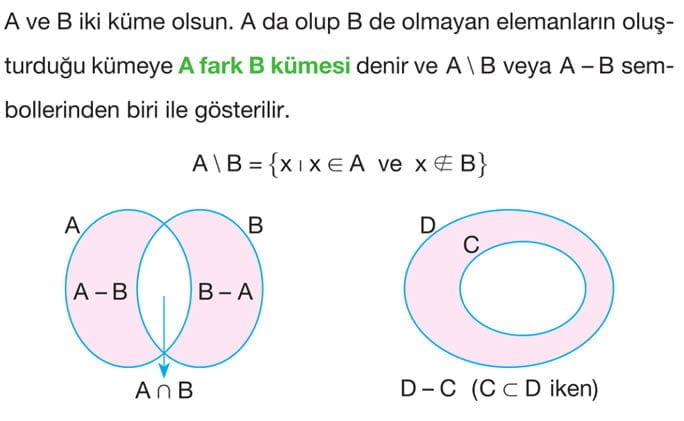
Kümelerde Fark İşlemi

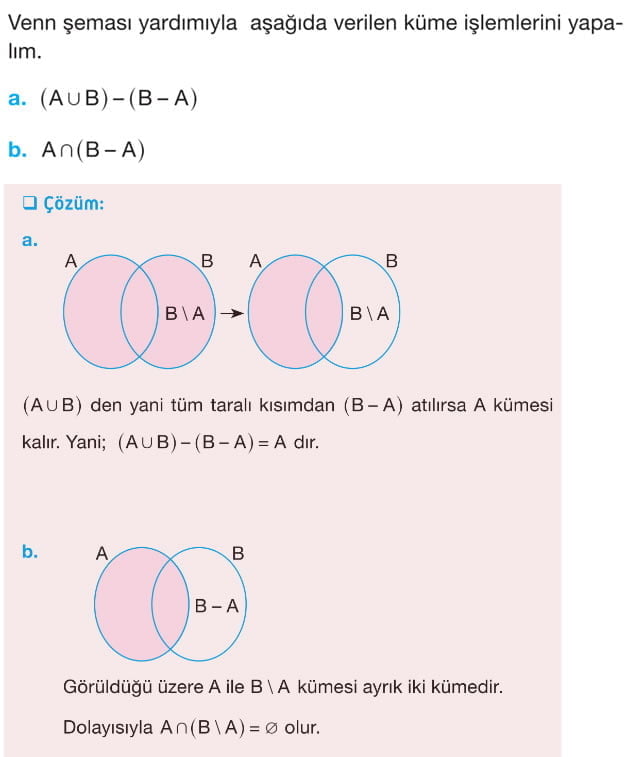
Örnek:

Kümelerde Fark İşleminin Özellikleri

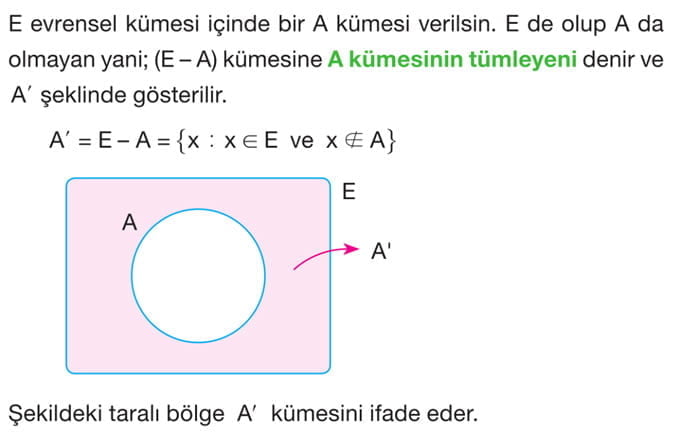
Kümelerde Tümleme İşlemi

Kümelerde Tümleme İşleminin Özellikleri

Kümeler ile Sembolik Mantık Arasındaki İlişki

Kümelerde İşlemler Çözümlü Sorular

Kümelerde İşlemler Video

Kümelerde kesişim, birleşim, fark ve tümleme işlemleri, De Morgan kuralları gibi konseptler matematikte önemli bir rol oynar. İşte bu konuların daha ayrıntılı bir konu anlatımı:

Kümelerde İşlemler:

Kesişim: İki veya daha fazla kümenin aynı öğelerini içeren yeni bir küme oluşturur. Kesişim işareti "∩" ile gösterilir. Örnek:

• A = {1, 2, 3, 4}
• B = {3, 4, 5, 6}
• A ∩ B = {3, 4} (A ve B'nin kesişimi)

Birleşim: İki veya daha fazla kümenin tüm öğelerini içeren yeni bir küme oluşturur. Birleşim işareti "∪" ile gösterilir. Örnek:

• A = {1, 2, 3, 4}
• B = {3, 4, 5, 6}
• A ∪ B = {1, 2, 3, 4, 5, 6} (A ve B'nin birleşimi)

Fark: İki kümenin farkı, birinci kümedeki öğelerden ikinci kümedeki öğeleri çıkartarak elde edilen yeni bir kümedir. Fark işareti "−" veya "" ile gösterilir. Örnek:

• A = {1, 2, 3, 4}
• B = {3, 4, 5, 6}
• A - B = {1, 2} (A'nın B'ye göre farkı)

Tümleme: Bir kümenin evrensel kümeden çıkarılması ile elde edilen kümedir. Tümleme işareti "′" veya "c" ile gösterilir. Örnek:

• U = {1, 2, 3, 4, 5, 6}
• A = {3, 4}
• A' = {1, 2, 5, 6} (A'nın tümlemesi)

De Morgan Kuralları: De Morgan kuralları, küme işlemleri ile ilgili önemli kurallardır ve işlemleri daha kolay yapmayı sağlar. İşte De Morgan kuralları:

• De Morgan'ın İlk Kural: İki kümenin birleşiminin tümlemesi, bu iki kümenin tümlemelerinin kesişimine eşittir. Yani (A ∪ B)' = A' ∩ B'.
• De Morgan'ın İkinci Kural: İki kümenin kesişiminin tümlemesi, bu iki kümenin tümlemelerinin birleşimine eşittir. Yani (A ∩ B)' = A' ∪ B'.

Bu kurallar, karmaşık küme işlemlerini daha basit bir şekilde ifade etmek ve işlem yapmak için kullanılır. Kümelerde işlemler ve De Morgan kuralları, matematiksel düşünme becerilerini geliştirmek ve karmaşık ifadeleri daha basit bir şekilde ifade etmek için önemlidir. Bu konuları öğrenerek, problemleri daha etkili bir şekilde çözebilirsiniz.

Soru 1: Kesişim İşlemi A = {1, 2, 3, 4, 5} B = {3, 4, 5, 6, 7}
A ve B kümelerinin kesişimini (A ∩ B) bulun.
Çözüm 1: A ∩ B, A ve B kümelerinin ortak öğelerini içerir. Ortak öğeler {3, 4, 5} olduğundan, A ∩ B = {3, 4, 5}

Soru 2: Birleşim İşlemi C = {1, 2, 3, 4} D = {3, 4, 5, 6, 7}
C ve D kümelerinin birleşimini (C ∪ D) bulun.
Çözüm 2: C ∪ D, C ve D kümelerinin tüm öğelerini içerir. C ve D kümelerinin birleşimi şu şekildedir: C ∪ D = {1, 2, 3, 4, 5, 6, 7}

Soru 3: Fark İşlemi E = {1, 2, 3, 4, 5} F = {3, 4, 5, 6, 7}
E ve F kümelerinin farkını (E - F) bulun.
Çözüm 3: E - F, E kümesinde bulunan ancak F kümesinde bulunmayan öğeleri içerir. E ve F kümelerinin farkı şu şekildedir: E - F = {1, 2}

Soru 4: Tümleme İşlemi G = {1, 2, 3, 4, 5, 6, 7} H = {2, 4, 6}
G kümesinin H kümesinin tümlemesini (G - H) bulun.
Çözüm 4: G - H, G kümesinde bulunan ancak H kümesinde bulunmayan öğeleri içerir. G kümesinin H kümesinin tümlemesi şu şekildedir: G - H = {1, 3, 5, 7}

Etkinlik: Karmaşık Küme İşlemleri Öğrencilere karmaşık küme işlemleri içeren sorular verin. Örneğin, A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {2, 3, 4, 7} gibi kümelerin birleşimini, kesişimini, farkını ve tümlmesini bulmalarını isteyebilirsiniz.