Önermeler 9. Sınıf Matematik
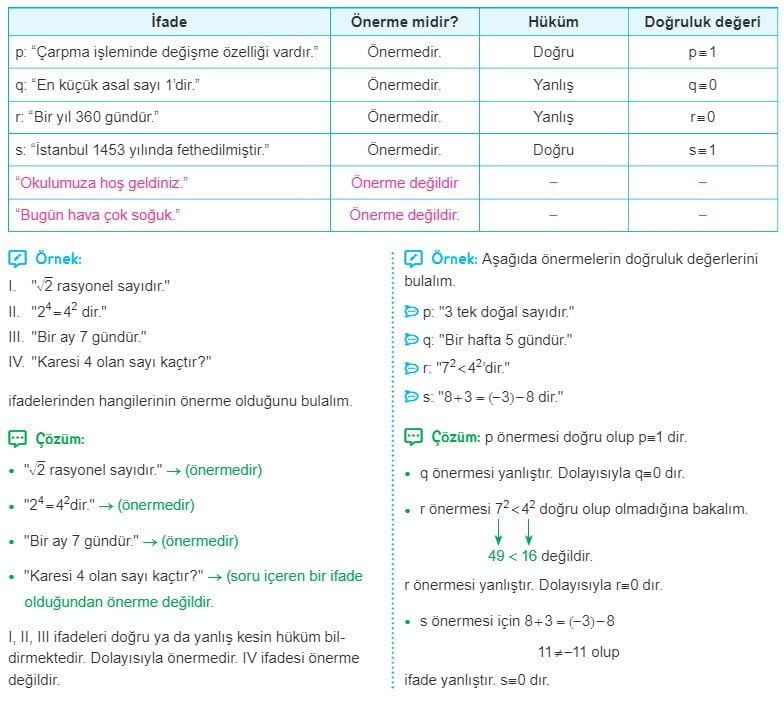
- Doğru ya da yanlış kesin hüküm bildiren ifadelere önerme denir.
| İfade | Önerme midir? | Hüküm |
|---|---|---|
| “Türkiye’nin başkenti Ankara’dır.” | Önermedir. | Doğru |
| “Türkiye’nin başkenti İstanbul’dur.” | Önermedir. | Yanlış |
| “Akşam eve erken gel.” | Önerme değildir. | (Emir) |
| “Yarın gidecek misiniz?” | Önerme değildir. | (Soru) |
| “Hafta sonu sinemaya gidelim.” | Önerme değildir. | (İstek) |
| “Bugün çok mutluyum.” | Önerme değildir. | (Heyecan) |
Soru, istek, emir, heyecan ve görecelik anlamları içeren ifadeler önerme değildir.
- Önermeler gibi küçük harflerle gösterilir.
- Önermenin bildirdiği hükümlere doğruluk değeri denir. Önermenin hükmü doğru ise 1 veya D, yanlış ise 0 veya Y ile gösterilir.
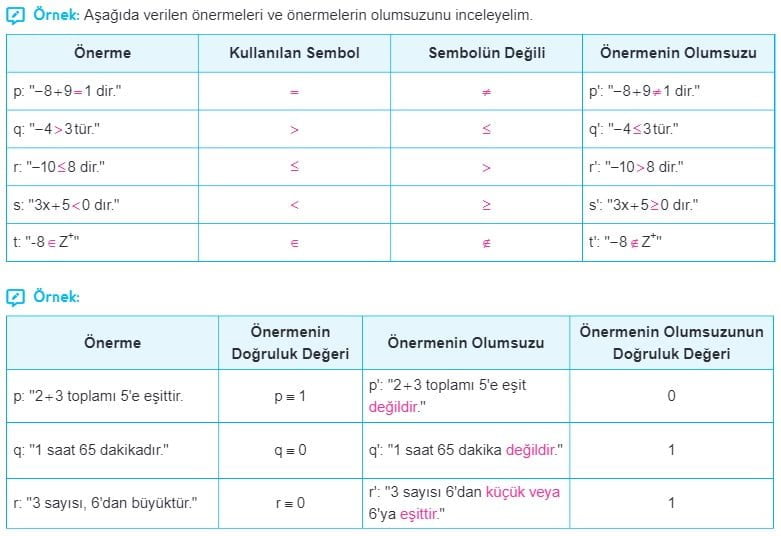
- Doğruluk değerleri önermeden sonra konulan “≡“ işareti ile gösterilir.







Önermenin Değili (Olumsuzu)

Önermeler Çözümlü Sorular
Önermeler Video
9. Sınıf Önermeler Konu Anlatımı Çözümlü Sorular Örnekler
Önermeler, matematiksel mantığın temel yapı taşlarından biridir ve doğru ya da yanlış kesin bir hüküm bildiren ifadelerdir. 9. sınıf matematik müfredatında, öğrenciler önermeler kavramını, önermelerin doğruluk değerlerini ve mantık işlemlerini öğrenirler. Bu konular, matematiksel düşünme ve problem çözme becerilerini geliştirmek için kritik öneme sahiptir.
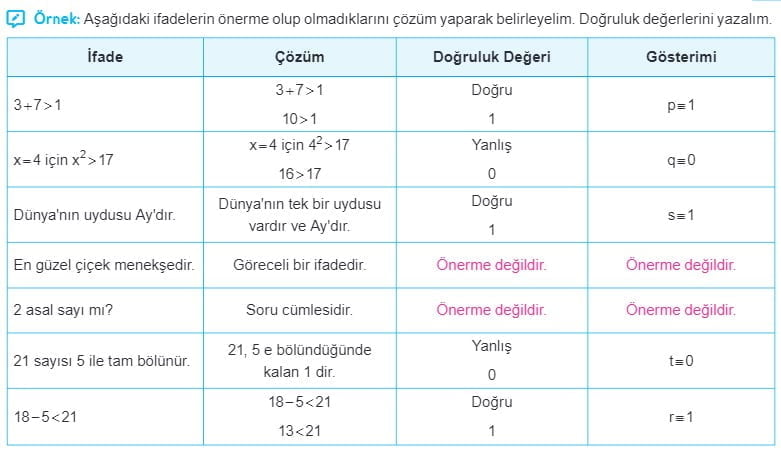
Bir önerme, kesin bir doğruluk değeri olan ifadeye denir. Örneğin, "Türkiye'nin başkenti Ankara'dır." ifadesi doğru bir önerme iken, "Türkiye'nin başkenti İstanbul'dur." ifadesi yanlış bir önermedir. Önerme olmayan ifadeler ise kesin bir doğruluk değeri taşımayan emir, istek, soru veya heyecan bildiren ifadelerdir. Örneğin, "Akşam eve erken gel." (emir), "Yarın gidecek misiniz?" (soru) ve "Bugün çok mutluyum." (heyecan) gibi ifadeler önerme değildir.
Önerme Nedir? Önermeler, bir şeyin doğru veya yanlış olduğunu ifade eden ifadelerdir. Matematikte, önermeler "P," "Q," veya başka harf veya sembollerle temsil edilir. Örnekler:
- "3 bir tek sayıdır" bir önermedir ve doğrudur.
- "2 + 2 = 5" bir önermedir ve yanlıştır.
- "x > 5" bir önermedir ve x'in değerine bağlı olarak doğru veya yanlış olabilir.
Bağlaçlar ve Önerme İlişkisi Bağlaçlar, önermeleri birleştirmek veya ilişkilendirmek için kullanılır. Temel bağlaçlar şunlardır:
- "ve" (veya "and"): P ve Q (Hem P hem de Q doğru olmalıdır).
- "veya" (veya "or"): P veya Q (P veya Q'dan en az biri doğru olmalıdır).
- "değil" (veya "not"): Değil P (P'nin tersi veya zıttı).
Önerme Tabloları Önerme tabloları, bağlaçların ve önermelerin doğruluk değerlerini gösterir. Örnek olarak, "ve" (and) bağlacını kullanarak bir önerme tablosu oluşturulabilir:
| P | Q | P ve Q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Bu tablo, "ve" bağlacının çalışma mantığını gösterir. Her bir sütun, farklı önerme değerlerini temsil eder.
Öğrencilere bu temel önerme mantığı kavramlarını ve önerme tablolarını anlatarak, matematiksel düşünme ve mantık becerilerini geliştirmelerine yardımcı olabilirsiniz. Örnekler ve uygulamalarla öğrencilerin anlayışlarını pekiştirmek önemlidir.
Önerme, bir şeyin doğru veya yanlış olduğunu ifade eden bir ifadedir. Matematik ve mantık alanlarında önemli bir kavramdır ve öğrencilerin mantıklı düşünme yeteneklerini geliştirmelerine yardımcı olur. İşte önermenin tanımı ve örnekler:
Önerme Tanımı: Önerme, bir ifadenin ya doğru (1) ya da yanlış (0) olduğu bir ifadedir. Önerme, kesin bir şekilde belirli bir durumu veya koşulu açıklar.
Önerme Örnekleri:
- "2 + 2 = 4" bir önermedir ve doğrudur. (1)
- "3 çift bir sayıdır" bir önermedir ve doğrudur. (1)
- "Güneş her zaman parlardır" bir önerme değildir, çünkü bu ifade her zaman doğru veya yanlış değildir. (0 veya 1)
- "5 < 3" bir önermedir ve yanlıştır. (0)
- "x > 7" bir önermedir, ancak x'in değerine bağlı olarak doğru veya yanlış olabilir. Örneğin, x = 8 için doğrudur, ancak x = 6 için yanlıştır. (0 veya 1)
Önermeler, matematiksel ifadeler, geometrik açıklamalar, bilimsel ifadeler ve daha birçok farklı bağlamda kullanılabilir. Öğrenciler, önermeleri tanımak ve değerlendirmek konusunda beceri geliştirdikçe, mantıklı düşünme yeteneklerini güçlendirebilirler.
Soru 1: Önermelerin İşlenmesi Aşağıdaki önermeyi inceleyin ve doğru veya yanlış olduğunu belirleyin: Önerme: "Eğer bir üçgen dik ise, o zaman üçgenin hipotenüsü en uzun kenarıdır."
Çözüm 1: Bu önerme doğrudur. Dik üçgenlerin hipotenüsü, diğer iki kenardan daha uzundur ve bu geometrik bir gerçektir.
Soru 2: Bağlaçlar ve Önerme Tablosu Aşağıdaki önermeleri ve bağlaçları kullanarak önerme tabloları oluşturun:
- P: Bugün hava güzel.
- Q: Ben dışarıya çıkıyorum.
- R: Akşam oluyor.
Bağlaçlar:
- P ve Q
- Q veya R
- Değil P
- P → Q (P ise Q)
- P ↔ Q (P ile Q eşit)
Çözüm 2:
- P: Bugün hava güzel.
- Q: Ben dışarıya çıkıyorum.
- R: Akşam oluyor.

















