Kümelerde Birleşim İşlemi

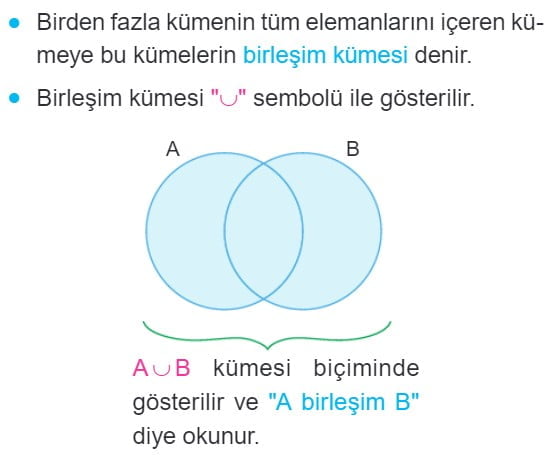
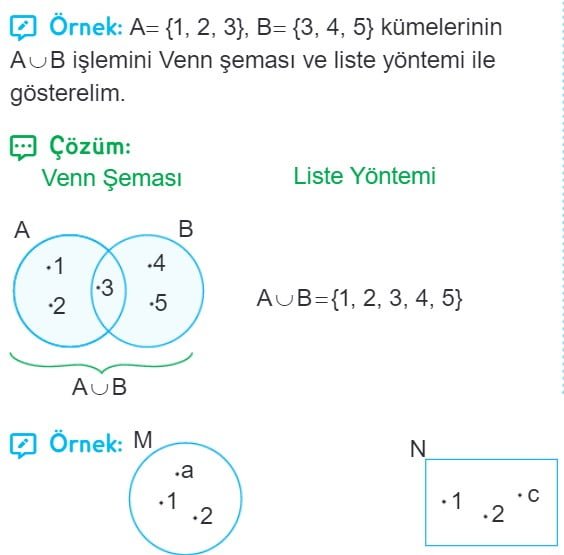
Kümelerde Kesişim İşlemi

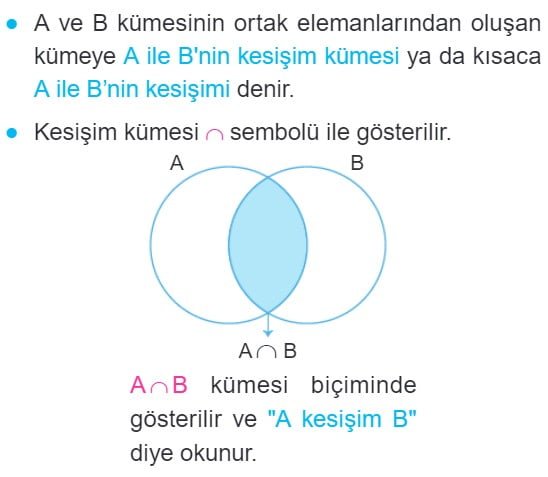
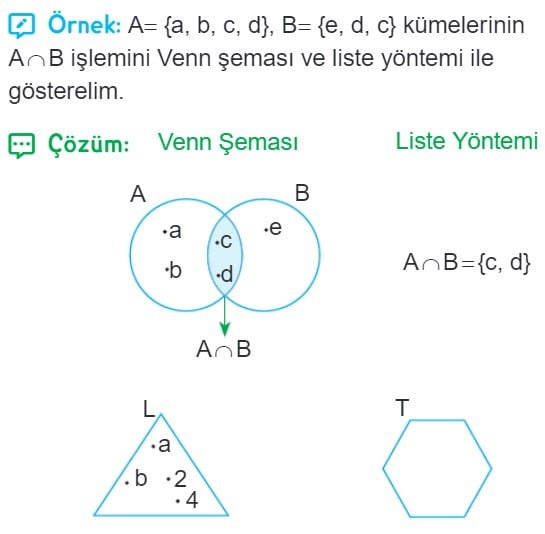
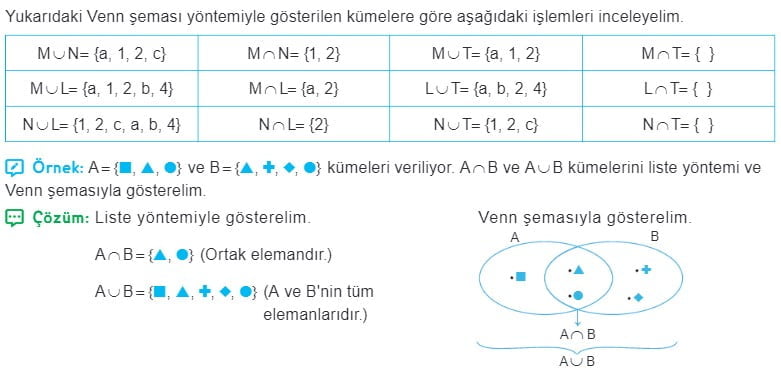
Kümelerde Birleşim ve Kesişim Soru Çözümleri

Kümelerde Birleşim ve Kesişim Video

6. sınıf öğrencileri için kümelerde birleşim ve kesişim işlemi konu anlatımı şu şekildedir:

Kümelerde Birleşim (Union) İşlemi:

• Birleşim işlemi, iki veya daha fazla kümenin öğelerini toplar ve her bir öğeyi yalnızca bir kez içeren yeni bir küme oluşturur.
• Birleşim işlemi sembolü "∪" ile gösterilir.

Örnek 1: A = {1, 2, 3, 4, 5} B = {3, 4, 5, 6, 7} A ∪ B = {1, 2, 3, 4, 5, 6, 7}

Kümelerde Kesişim (Intersection) İşlemi:

• Kesişim işlemi, iki veya daha fazla kümenin ortak öğelerini bulur ve bu ortak öğeleri içeren yeni bir küme oluşturur.
• Kesişim işlemi sembolü "∩" ile gösterilir.

Örnek 2: A = {2, 4, 6, 8, 10} B = {3, 6, 9, 12, 15} A ∩ B = {6}

Birleşim ve Kesişim İşlemlerinin Kullanımı:

• Birleşim işlemi, iki kümenin bir araya getirilmesini temsil eder. Örneğin, iki farklı grup öğrencinin hangi konularda ortak ilgi veya özelliklere sahip olduğunu belirlemek için kullanılabilir.
• Kesişim işlemi, iki kümenin ortak öğelerini bulur ve bu öğeler üzerine odaklanmayı temsil eder. Örneğin, iki kitap listesi arasındaki ortak kitapları belirlemek için kullanılabilir.

Örnek 3: A = {kırmızı, yeşil, mavi, sarı} B = {mavi, sarı, pembe, turuncu} A ∪ B = {kırmızı, yeşil, mavi, sarı, pembe, turuncu} A ∩ B = {mavi, sarı}

Birleşim ve kesişim işlemleri, matematikte ve gerçek hayatta çok çeşitli problemleri çözmek için kullanılır. İki veya daha fazla kümenin öğelerini bir araya getirmek veya belirli özelliklere sahip öğeleri seçmek için bu işlemleri kullanmak, verileri düzenlemek ve kararlar almak için önemlidir.

Soru 1: A = {1, 2, 3, 4, 5} B = {3, 4, 5, 6, 7} C = {5, 6, 7, 8, 9}

A, B ve C kümelerinin birleşimi (A ∪ B ∪ C) nedir?

Çözüm: A ∪ B ∪ C, bu üç kümenin öğelerini toplar ve her bir öğeyi yalnızca bir kez içeren yeni bir küme oluşturur. A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 9}

Soru 2: D = {2, 4, 6, 8, 10} E = {3, 6, 9, 12, 15} F = {5, 10, 15, 20, 25}

D, E ve F kümelerinin kesişimi (D ∩ E ∩ F) nedir?

Çözüm: D ∩ E ∩ F, bu üç kümenin ortak öğelerini bulur ve yeni bir küme oluşturur. D ∩ E ∩ F = {6}

Etkinlik 1: Öğrencilere farklı kümelerin öğelerini içeren kartlar verin. Her öğrenci rastgele bir kart alsın ve diğer öğrencilere kendi kartları ile ilgili birleşim veya kesişim sorusu sorsun. Diğer öğrenciler bu soruları yanıtlayarak doğru sonuçları bulmaya çalışsınlar.

Etkinlik 2: Öğrencilere belirli özelliklere sahip nesneleri temsil eden farklı kümeler verin. Öğrencilerden bu kümelerin birleşimini ve kesişimini bulmalarını isteyin ve sonuçları sınıfta paylaşmalarını sağlayın.

Etkinlik 3: Öğrencilere rastgele iki veya daha fazla küme verin ve bu kümelerin birleşimini ve kesişimini hesaplamalarını isteyin. Daha sonra öğrencilere bu işlemleri gerçek hayattaki senaryolarda nasıl kullanabilecekleri sorusunu sorarak uygulama yapmalarını sağlayın.

Bu tür sorular ve etkinlikler, öğrencilerin kümelerde birleşim ve kesişim işlemini anlamalarına ve uygulamalarına yardımcı olur. Ayrıca, matematiksel düşünme becerilerini geliştirir ve problem çözme yeteneklerini artırır.