Küme Kavramı

Küme Gösterme Yöntemleri

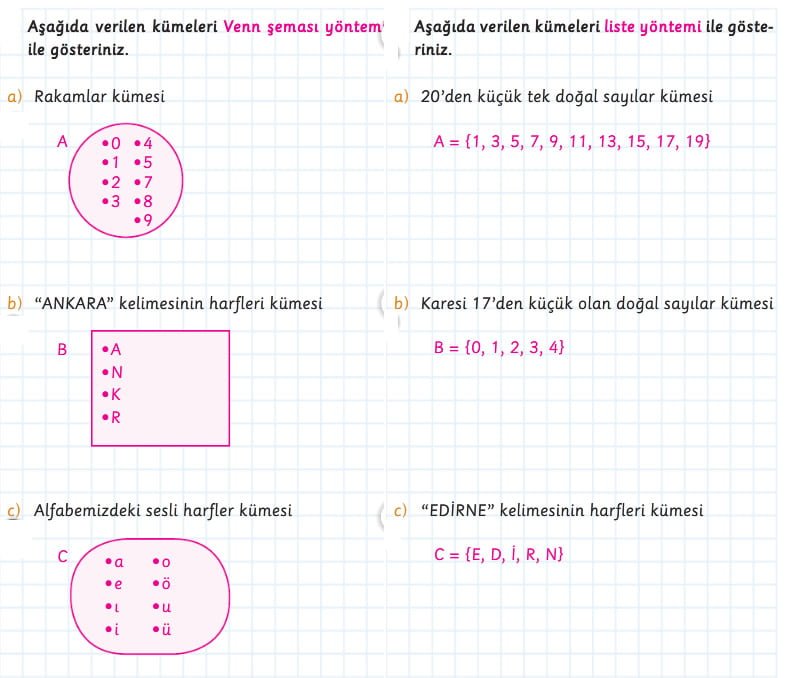
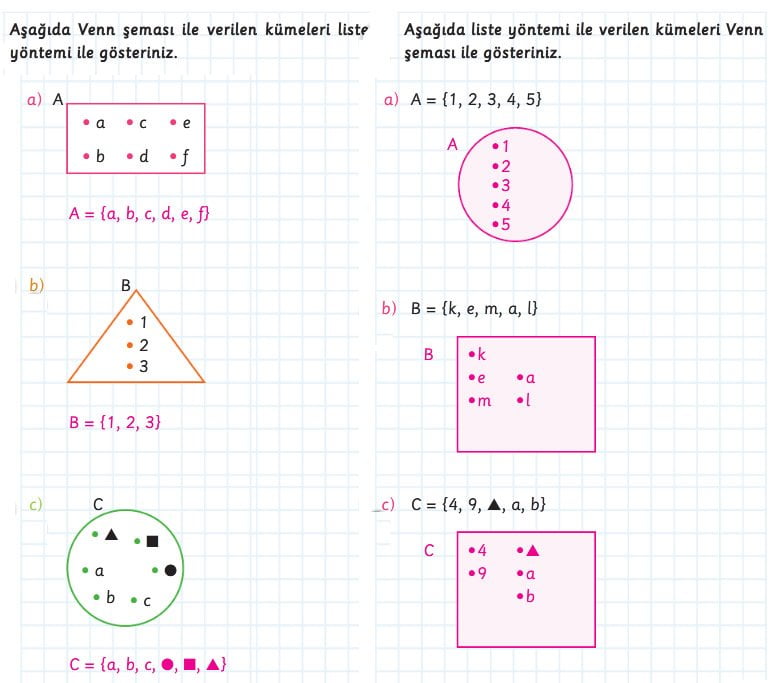
Küme Gösterim Yöntemlerinin Birbirine Dönüştürülmesi

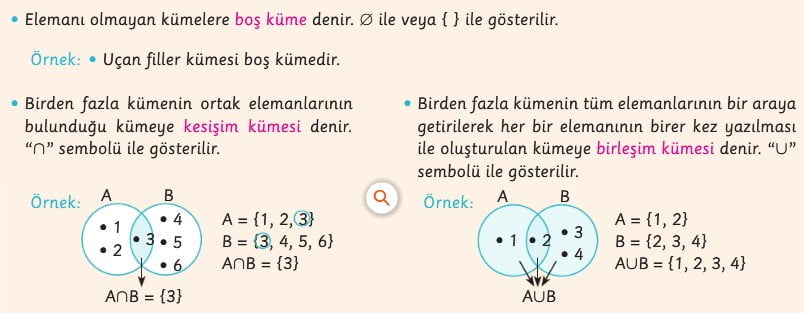
Boş Küme – Birleşim Kümesi – Kesişim Kümesi

Kümeler Soru Çözümleri

Kümeler Video

Küme Nedir?

• Bir küme, nesnelerin veya öğelerin bir araya getirildiği bir matematiksel kavramdır. Öğeler, kümenin elemanları olarak adlandırılır.

Küme Temsili:

• Bir küme, genellikle süslü parantezler {} veya küme sembolü ile temsil edilir. Örneğin, A = {1, 2, 3, 4, 5} şeklinde bir küme gösterimi kullanılabilir.

Küme Elemanları:

• Bir kümenin öğelerine eleman denir. Öğeler, sayılar, harf, nesneler veya başka türde nesneler olabilir.

Örnek 1: A = {1, 2, 3, 4, 5} Bu küme, 1, 2, 3, 4 ve 5 gibi beş öğeye sahiptir.

Sıralı Küme ve Sırasız Küme:

• Bir sıralı küme, öğelerin belirli bir sırayla listelendiği bir küme türüdür. Öğelerin sırası önemlidir.
• Bir sırasız küme, öğelerin sırasının önemli olmadığı bir küme türüdür. Öğeler rastgele sırayla listelenir.

Örnek 2: Sıralı Küme (2, 4, 6, 8, 10) bir sıralı kümedir, çünkü öğeler belirli bir sırayla listelenir.

Örnek 3: Sırasız Küme {4, 10, 6, 2, 8} bir sırasız kümedir, çünkü öğelerin sırası önemli değildir.

Alt Küme (Alt Kümeler):

• Bir kümenin alt kümesi, bu küme içindeki öğelerin bir alt kümesidir. Örneğin, {1, 2} A kümesinin bir alt kümesidir.

Boş Küme:

• Hiçbir öğeyi içermeyen bir küme boş kume olarak adlandırılır ve sembolü "∅" veya "{}" ile gösterilir.

Evrensel Küme:

• Evrensel küme, bir problemin çözümü için düşünülen tüm öğelerin toplamını ifade eder ve sembolü "U" ile gösterilir.

Kümeler, matematikte ve problem çözmede önemli bir rol oynar. Küme operasyonları, sayılarla ve verilerle çalışırken sıkça kullanılır ve matematiksel düşünme becerilerini geliştirir. Kümelerin temel kavramları, sayılar, mantık ve veri analizi gibi birçok matematiksel konunun temelini oluşturur.

Soru 1: A = {1, 2, 3, 4, 5} B = {3, 4, 5, 6, 7}

A ve B kümelerinin birleşimini (A ∪ B) ve kesişimini (A ∩ B) bulun.

Çözüm:

• A ∪ B (Birleşim): A ∪ B, A ve B kümelerinin öğelerini toplar ve tekrarlanan öğeleri yalnızca bir kez ekler. A ∪ B = {1, 2, 3, 4, 5, 6, 7}
• A ∩ B (Kesişim): A ∩ B, A ve B kümelerinin ortak öğelerini bulur. A ∩ B = {3, 4, 5}

Etkinlik 1: Küme Gösterimleri Öğrencilere farklı kümelerin sembollerini ve öğelerini içeren kartlar verin. Öğrencilerden bu kümelerin sembollerini tanımlamalarını ve öğelerini listelemelerini isteyin.

Etkinlik 2: Küme Operasyonları Bulmacası Öğrencilere birleşim ve kesişim işlemlerini içeren bir bulmaca verin. Öğrenciler, verilen kümeleri kullanarak doğru sonuçları bulmaya çalışsınlar.

Etkinlik 3: Küme Karşılaştırma Öğrencilere farklı kümelerin sembollerini ve öğelerini içeren kartlar verin. Her öğrenci rastgele bir kart alsın ve diğer öğrencilere kendi kartları ile ilgili birleşim veya kesişim sorusu sorsun. Diğer öğrenciler bu soruları yanıtlayarak doğru sonuçları bulmaya çalışsınlar.

Bu tür etkinlikler, öğrencilerin kümeleri anlamalarına ve kümelerle ilgili işlemleri öğrenmelerine yardımcı olur. Ayrıca, matematiksel düşünme becerilerini geliştirir ve kümelerin günlük yaşamda nasıl kullanılabileceği konusunda fikir sahibi olmalarına yardımcı olur.