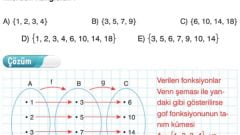
10. Sınıf Fonksiyonlarda Bileşke İşlemi Konu Anlatımı ve Çözümlü Sorular Matematik
Birebir ve Örten Fonksiyon
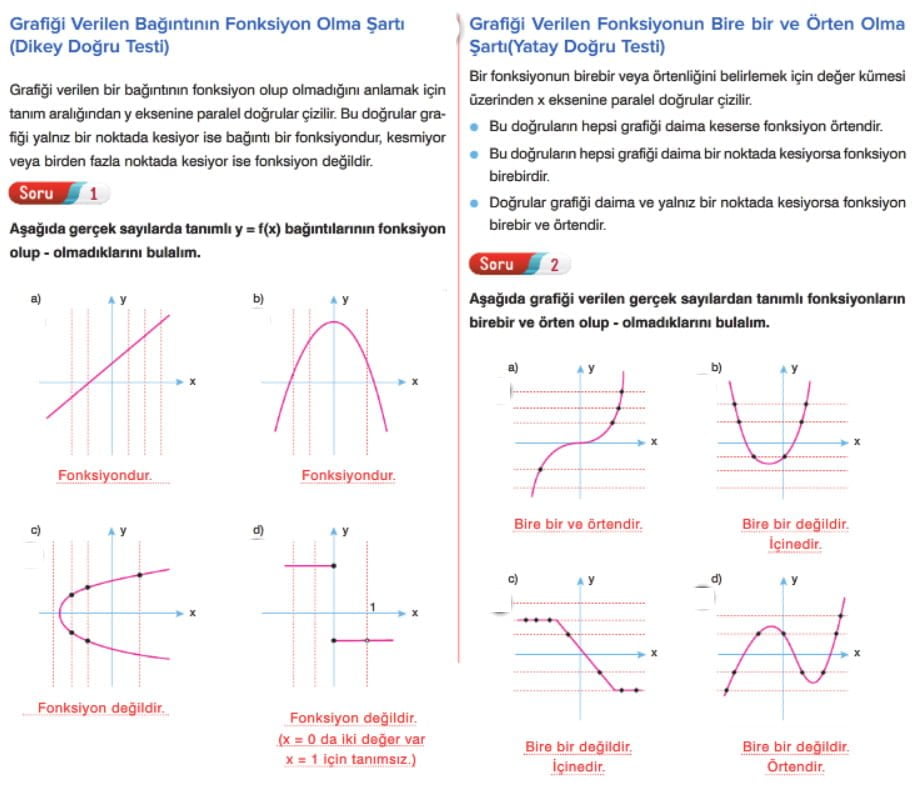
Fonksiyonlarda Bileşke İşlemi
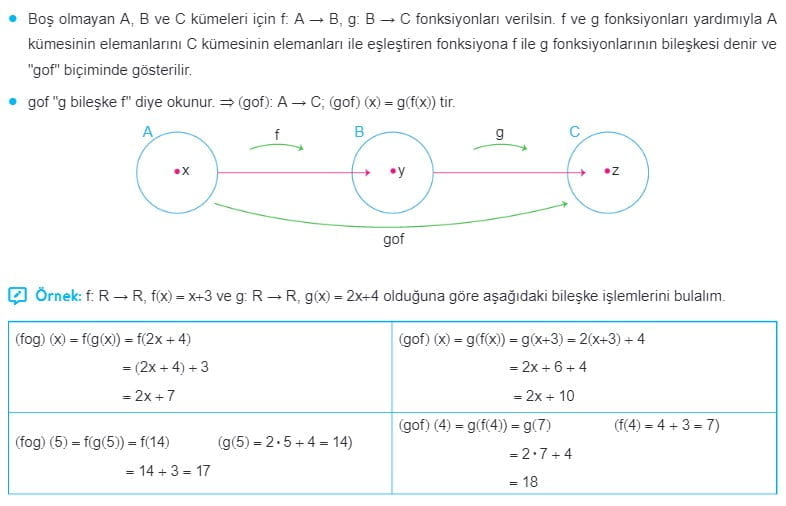

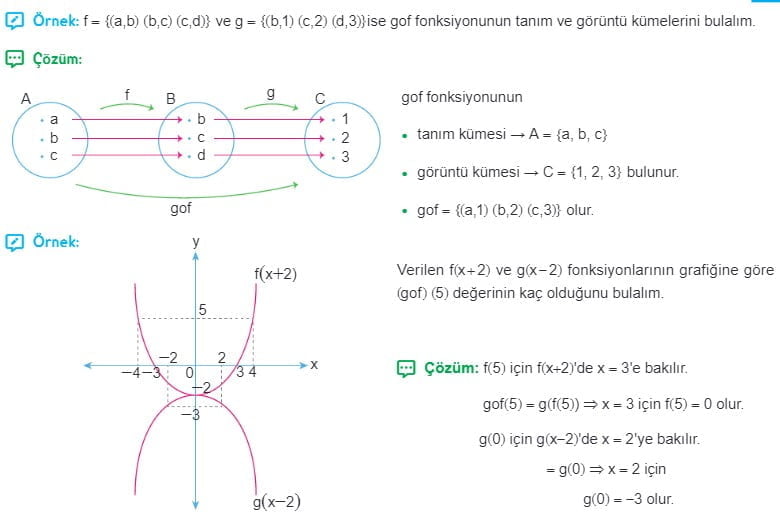

Fonksiyonlarda Bileşke İşlemi Çözümlü Sorular
Fonksiyonlarda Bileşke İşlemi Video
10. Sınıf Bileşke Fonksiyon Konu Anlatımı Çözümlü Sorular Konu Özeti
Birebir ve örtenlik, matematikte kullanılan iki önemli kavramdır.
Birebir fonksiyon, her bir f(x) değerine karşılık gelen tek bir x değeri olan fonksiyondur.
Örten fonksiyon, her bir x değerine karşılık gelen bir f(x) değeri olan fonksiyondur.
Birebir ve örten fonksiyon, hem birebir hem de örten olan fonksiyondur.
Birebir fonksiyonlarda,
- Her bir f(x) değerine karşılık gelen tek bir x değeri vardır.
- f(x1) = f(x2) ise x1 = x2 olur.
Örten fonksiyonlarda,
- Her bir x değerine karşılık gelen bir f(x) değeri vardır.
- X kümesi üzerinde birebir bir dönüşüm vardır.
Birebir ve örten fonksiyonlarda,
- Her bir f(x) değerine karşılık gelen tek bir x değeri vardır.
- X kümesi üzerinde birebir bir dönüşüm vardır.
Birebir ve örten fonksiyonların örnekleri şunlardır:
- Y = x fonksiyonu birebir ve örten bir fonksiyondur.
- Y = x^2 fonksiyonu birebir ancak örten değildir.
- Y = |x| fonksiyonu örten ancak birebir değildir.
Birebir ve örten fonksiyonların uygulamaları şunlardır:
- Birebir ve örten fonksiyonlar, kodlama ve şifreleme işlemlerinde kullanılır.
- Birebir ve örten fonksiyonlar, matematiksel modelleme işlemlerinde kullanılır.
- Birebir ve örten fonksiyonlar, istatistiksel analiz işlemlerinde kullanılır.
Birebir ve örten fonksiyonların özelliklerini anlamamız, bu fonksiyonların kullanıldığı alanlarda daha başarılı olmamızı sağlar.
Bileşik fonksiyon, iki veya daha fazla fonksiyonun bir araya getirilmesiyle oluşan fonksiyondur.
Bileşik fonksiyonlar, aşağıdaki şekilde tanımlanır:
g(f(x))
Bu ifadede, g(x) ve f(x) iki fonksiyondur. g(f(x)) ifadesi, f(x) fonksiyonunun çıktısını g(x) fonksiyonuna girdi olarak vererek elde edilen fonksiyonu ifade eder.
Bileşik fonksiyonların bazı örnekleri şunlardır:
- f(x) = x^2 ve g(x) = 2x fonksiyonlarının bileşkesi, g(f(x)) = 2(x^2) = 2x^2 fonksiyonudur.
- f(x) = x + 1 ve g(x) = x^2 fonksiyonlarının bileşkesi, g(f(x)) = (x + 1)^2 = x^2 + 2x + 1 fonksiyonudur.
Bileşik fonksiyonların özellikleri şunlardır:
- Bileşik fonksiyonlar, her zaman bir fonksiyondur.
- Bileşik fonksiyonun tanım kümesi, iç fonksiyonun tanım kümesidir.
- Bileşik fonksiyonun değer kümesi, dış fonksiyonun değer kümesidir.
Bileşik fonksiyonların uygulamaları şunlardır:
- Bileşik fonksiyonlar, matematiksel modelleme işlemlerinde kullanılır.
- Bileşik fonksiyonlar, istatistiksel analiz işlemlerinde kullanılır.
- Bileşik fonksiyonlar, bilgisayar bilimlerinde kullanılır.
Bileşik fonksiyonların özelliklerini anlamamız, bu fonksiyonların kullanıldığı alanlarda daha başarılı olmamızı sağlar.
1. Soru
f(x) = x^2 ve g(x) = 2x fonksiyonlarının bileşkesi nedir?
Çözüm:
g(f(x)) = 2(f(x)) = 2(x^2) = 2x^2
Cevap: 2x^2
2. Soru
f(x) = x + 1 ve g(x) = x^2 fonksiyonlarının bileşkesi nedir?
Çözüm:
g(f(x)) = (f(x))^2 = (x + 1)^2 = x^2 + 2x + 1
Cevap: x^2 + 2x + 1
3. Soru
f(x) = x^2 ve g(x) = x^3 fonksiyonlarının bileşkesi nedir?
Çözüm:
g(f(x)) = (f(x))^3 = (x^2)^3 = x^6
Cevap: x^6
4. Soru
f(x) = x^2 ve g(x) = ln(x) fonksiyonlarının bileşkesi nedir?
Çözüm:
g(f(x)) = ln(f(x)) = ln(x^2) = 2ln(x)
Cevap: 2ln(x)