Aynı Çevre Uzunluğuna Sahip Farklı Geometrik Şekiller 4. Sınıf Matematik
Geometrik şekiller, matematikte sıkça karşılaştığımız ve günlük hayatta da birçok yerde gördüğümüz yapılardır. Bu şekillerin çevre uzunluğu, bir şeklin tüm kenarlarının toplam uzunluğudur. Ancak, aynı çevre uzunluğuna sahip farklı geometrik şekiller de olabilir. Bu, matematiğin ilginç ve düşündürücü yönlerinden biridir. Örneğin, bir kare ve bir dikdörtgenin çevre uzunlukları aynı olabilir, fakat bu şekillerin kenar uzunlukları ve genel görünümleri farklıdır. Bu ders, öğrencilerin aynı çevre uzunluğuna sahip farklı geometrik şekiller oluşturma ve karşılaştırma becerilerini geliştirmeye odaklanmaktadır. Bu sayede, öğrenciler çevre kavramını daha derinlemesine anlayacak ve geometrik şekillerin farklı yönlerini keşfetme fırsatı bulacaklardır.
Çevre Ölçme Konuları
- Kare ve Dikdörtgenin Çevre Uzunlukları (Kare ve Dikdörtgenin Çevre Uzunlukları ile Kenar Uzunlukları Arasındaki İlişki)
- Çevre Uzunluğu Aynı Olan Geometrik Şekiller Oluşturma
- Çevre Ölçme Problemleri
Aynı Çevre Uzunluğuna Sahip Farklı Geometrik Şekiller Konu Anlatımı
- Farklı geometrik şekillerin çevre uzunlukları birbirine eşit olabilir.
Örnek: Aşağıda noktalı kâğıtta verilen geometrik şekillerin çevre uzunluklarını bulup karşılaştıralım.
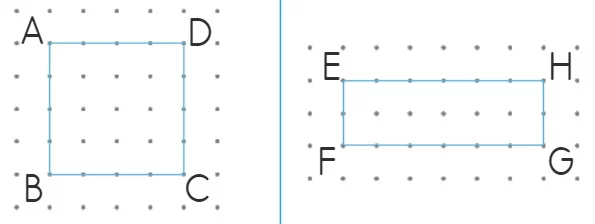
- ABCD bir kare: Çevre = 4 + 4 + 4 + 4 = 16 birim
EFGH bir dikdörtgen: Çevre = 2 + 6 + 2 + 6 = 16 birim
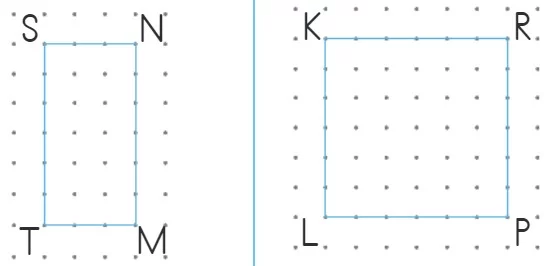
- STMN bir dikdörtgen: Çevre = 6 + 3 + 6 + 3 = 18 birim
KLPR bir kare: Çevre = 6 + 6 + 6 + 6 = 24 birim
Örnek: Aşağıda verilen birim kareli kâğıtlara çevre uzunlukları birbirine eşit olan farklı geometrik şekiller çizelim.
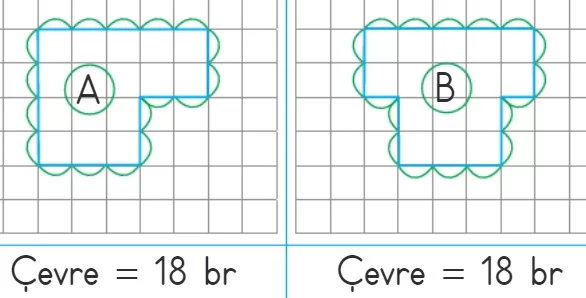
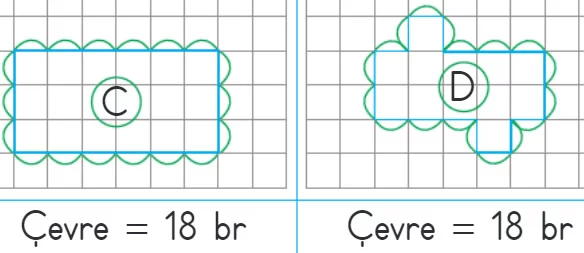
- A, B, C ve D farklı geometrik şekiller olmalarına rağmen çevre uzunlukları eşittir.
Örnek:
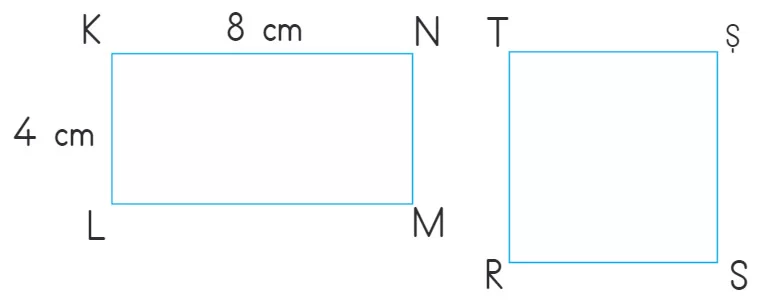
KLMN dikdörtgeninin çevre uzunluğu TRŞS karesinin çevre uzunluğuna eşittir. Buna göre karenin bir kenar uzunluğunu bulalım.
Çözüm:
- KLMN dikdörtgeninin çevre uzunluğu:
Çevre = 2 × (4 cm + 8 cm) = 2 × 12 cm = 24 cm - Karenin çevre uzunluğu bir kenarının 4 katına eşit olduğuna göre;
1 kenarın uzunluğu = 24 cm ÷ 4 = 6 cm’dir.
Örnek:
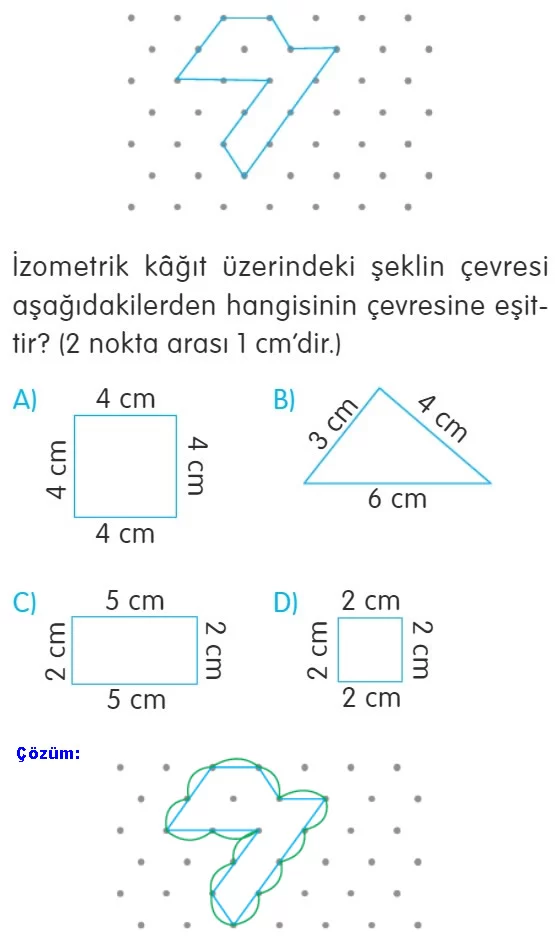
İzometrik kâğıtta verilen şeklin çevre uzunluğu 14 cm’dir.
Seçeneklerde bulunan dikdörtgenin çevresi 2 + 5 + 2 + 5 = 14 cm olup sağlamaktadır.
Aynı Çevre Uzunluğuna Sahip Farklı Geometrik Şekiller Çalışma Kağıdı ve Etkinlikler
Soru: Aşağıda verilen geometrik şekillerin çevre uzunluklarının eşit olduğu farklı geometrik şekilleri örnekteki gibi çiziniz.
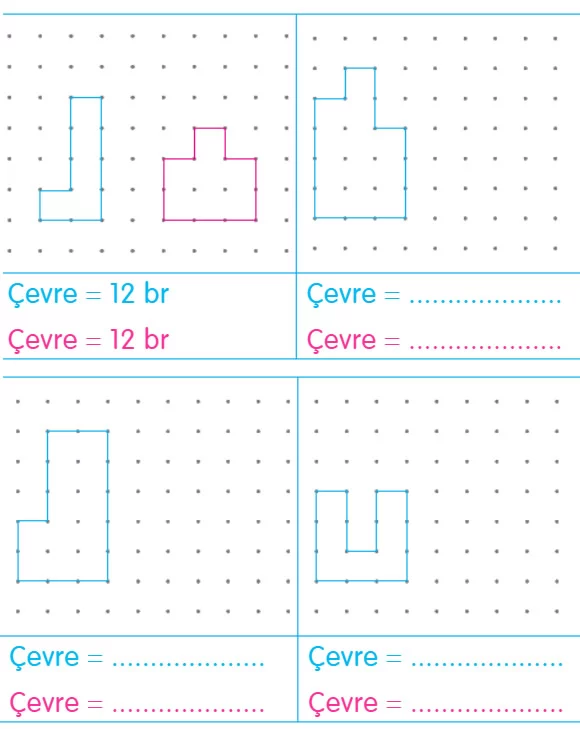
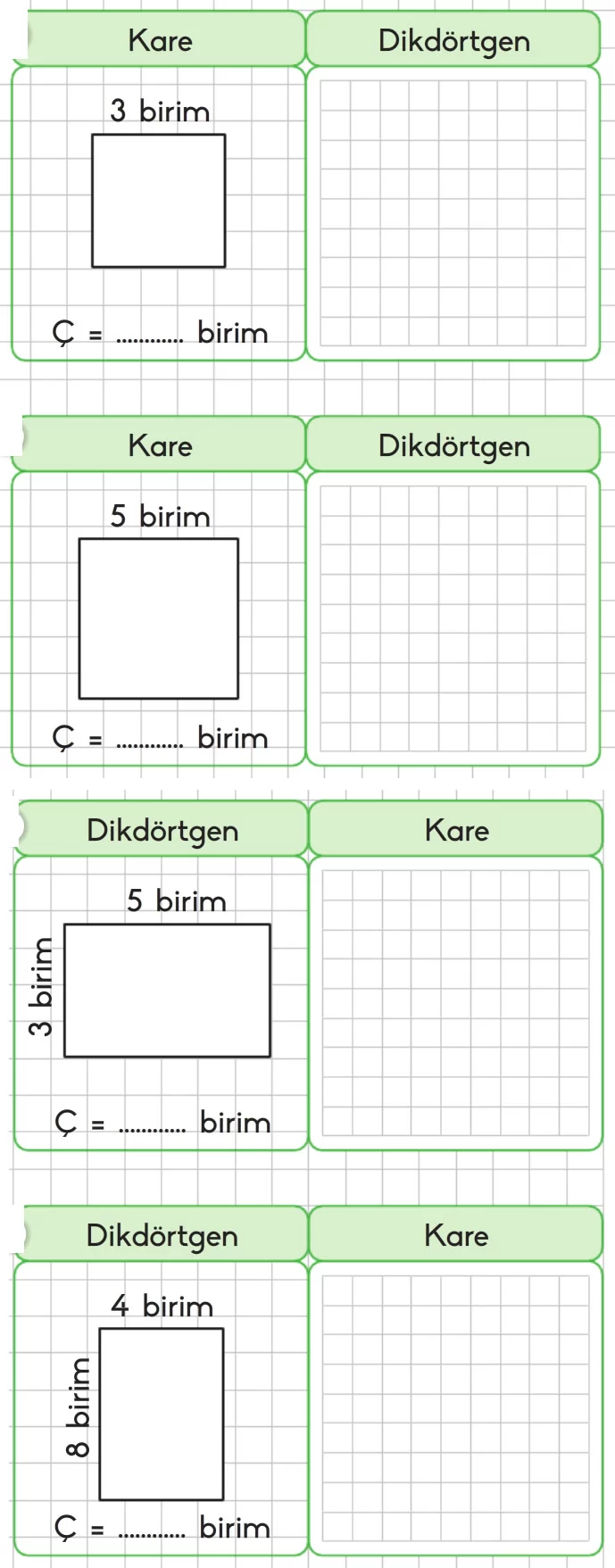
Soru: Aşağıdaki şekillerin çevre uzunluğunun kaç birim olduğunu bulalım. Aynı çevre uzunluğuna sahip istenilen şekli kareli alana çizelim.
Aynı Çevre Uzunluğuna Sahip Farklı Geometrik Şekiller Video
4. Sınıf Çevre Uzunluğu Aynı Olan Geometrik Şekiller Oluşturma Konu Anlatımı
Geometrik şekillerin çevre uzunluğu, bir şeklin tüm kenarlarının toplam uzunluğudur. Farklı şekiller, farklı kenar uzunluklarına sahip olmalarına rağmen, çevre uzunlukları eşit olabilir. Bu ders notu, aynı çevre uzunluğuna sahip farklı geometrik şekillerin nasıl oluşturulacağını ve karşılaştırılacağını öğretmek amacıyla hazırlanmıştır.
Çevre Uzunluğu Tanımı: Çevre uzunluğu, bir geometrik şeklin dış kenarlarının toplam uzunluğudur. Örneğin, bir karenin çevresi, tüm kenarlarının uzunluklarının toplanmasıyla bulunur.
Farklı Geometrik Şekillerle Çevre Uzunluğunun Eşitliği: Aynı çevre uzunluğuna sahip farklı şekiller çizilebilir. Örneğin, bir kare ve bir dikdörtgenin çevre uzunlukları aynı olabilir, ancak kenar uzunlukları farklıdır.
Örnek 1:
- Bir kare, kenar uzunlukları 4 birim olan dört kenardan oluşur. Bu karenin çevre uzunluğu 4 + 4 + 4 + 4 = 16 birimdir.
- Bir dikdörtgen, iki uzun kenarı 6 birim ve iki kısa kenarı 2 birim olan dört kenardan oluşur. Bu dikdörtgenin çevre uzunluğu 6 + 2 + 6 + 2 = 16 birimdir.
- Gördüğünüz gibi, kare ve dikdörtgenin çevre uzunlukları aynı olmasına rağmen, şekiller farklıdır.
Örnek 2:
- Bir kenar uzunluğu 8 cm olan dikdörtgenin çevre uzunluğunu hesaplayalım:
- Çevre = 2 x (8 cm + 4 cm) = 2 x 12 cm = 24 cm.
- Aynı çevre uzunluğuna sahip bir kare oluşturalım:
- Karenin çevre uzunluğu 24 cm olduğu için, bir kenar uzunluğunu bulmak için 24 ÷ 4 = 6 cm hesaplamasını yaparız.
Aktivite:
- Öğrencilerden, birim karelerle kaplanmış kâğıtlarda farklı şekiller oluşturmalarını ve bu şekillerin çevre uzunluklarını hesaplamalarını isteyin.
- Farklı şekillerin çevre uzunluklarının eşit olup olmadığını karşılaştırın.