Çarpanlara ayırma, polinomların daha küçük çarpanlara ayrılması sürecidir ve 9. sınıf matematik müfredatında önemli bir konudur. Bu makalede, tam kare ifadeler, özdeşlikler ve iki kare farkı üzerinde durulacak ve bu kavramlar hakkında detaylı bilgi verilecektir. Çarpanlara ayırma, denklem çözme, sadeleştirme ve integral hesaplama gibi birçok matematiksel işlemde temel bir rol oynar.

Tam Kare İfadeler

Tam kare ifadeler, bir binomun karesini ifade eder. İki temel tam kare özdeşliği şunlardır:

1. (a + b)² = a² + 2ab + b²
2. (a – b)² = a² – 2ab + b²

Bu özdeşlikler, bir ifadenin karesini alırken kullanılan önemli kurallardır. Örneğin:

Örnek:

$$(x+3{)}^2=x^2+2\cdot x\cdot 3+3^2=x^2+6x+9$$

Örnek:

$$(2x – 5)² = (2x)² – 2 \cdot 2x \cdot 5 + 5² = 4x² – 20x + 25$$

İki Kare Farkı

İki kare farkı, iki kareli terimin farkı olarak ifade edilir ve şu özdeşliğe dayanır:

$$a² – b² = (a + b)(a – b)$$

Bu özdeşlik, birçok polinomu çarpanlara ayırmak için kullanılır. Örneğin:

Örnek:

$$x² – 9 = (x + 3)(x – 3)$$

Örnek:

$$4x² – 25 = (2x + 5)(2x – 5)$$

Özdeşlikler

Özdeşlikler, iki ifadenin her durumda eşit olduğunu belirten matematiksel denklemlerdir. En yaygın özdeşliklerden bazıları şunlardır:

1. (a + b)² = a² + 2ab + b²
2. (a – b)² = a² – 2ab + b²
3. a² – b² = (a + b)(a – b)

Bu özdeşlikler, polinomları sadeleştirme ve çarpanlara ayırma süreçlerinde kullanılır.

Çarpanlara Ayırma Örnekleri

Örnek:

$$x^2+10x+25=(x+5{)}^2$$

Örnek:

$$x^2-16=(x+4)(x-4)$$

Örnek:

$$9x^2-30x+25=(3x-5{)}^2$$

Çarpanlara ayırma, tam kare ifadeler, iki kare farkı ve özdeşlikler, matematiksel işlemleri daha basit hale getiren önemli araçlardır. Bu konuların anlaşılması, öğrencilerin matematiksel düşünme ve problem çözme becerilerini geliştirmelerine yardımcı olur. Tam kare ifadeler, iki kare farkı ve özdeşlikler, polinomları çarpanlarına ayırmak ve matematiksel ifadeleri sadeleştirmek için kritik öneme sahiptir. Bu yöntemler, hem akademik başarıyı artırır hem de günlük hayatta karşılaşılan problemleri çözmede kullanılabilir.

Uygulama ve Problemler

Çarpanlara ayırma, polinomların daha basit çarpanlara ayrılması sürecidir ve bu süreç, çeşitli matematiksel problemleri çözmek için kullanılır. Örneğin, denklemlerin köklerini bulmak veya integral hesaplamalarını kolaylaştırmak için çarpanlara ayırma yöntemleri kullanılır.

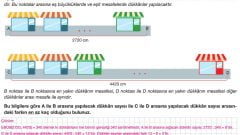
Örnek Problem:

$$(2x + 3)² - (x - 1)² = ?$$

Çözüm:

$$(2x + 3 + x - 1)(2x + 3 - (x - 1)) = (3x + 2)(x + 4)$$