Çarpma ve Bölme Arasındaki İlişki 4. Sınıf Matematik
Çarpma ve bölme işlemleri arasında güçlü bir ilişki vardır ve bu ilişki, matematikte problem çözme becerileri için hayati öneme sahiptir. Çarpma işlemi, tekrar eden toplama işlemi olarak düşünülebilirken, bölme işlemi bu toplamı belirli parçalara ayırma sürecidir. Bu ders, öğrencilerin çarpma ve bölme işlemleri arasındaki bağı anlamalarına ve bu iki işlemi birbirleriyle ilişkilendirerek problem çözme yeteneklerini geliştirmelerine yardımcı olur.
Önceki Konu: Bölme İşleminin Sonucunu Tahmin Etme
Sonraki Konu: Bölme İşlemi Problemleri
Çarpma ve Bölme Arasındaki İlişki Ders Notu
Çarpma ve bölme işlemi arasında nasıl bir ilişki vardır?
- Çarpma işleminin doğruluğunu kontrol etmek için bölme işlemi yaparız.
Örnek 1:
. 5 → Çarpan
× 4 → Çarpan
───────
20 → Çarpım
Doğruluğunu kontrol edelim;
20 ÷ 4 = 5
20 ÷ 5 = 4
- Bölme işleminin doğruluğunu kontrol etmek için çarpma işlemi yaparız.
Örnek 2:
32 ÷ 8 = 4
Bölünen → 32
Bölen → 8
Bölüm → 4
Bölen × Bölüm = Bölünen
8 × 4 = 32
Çarpma ve bölme arasındaki ilişkiden yararlanarak; çarpma ve bölme işlemlerinde verilmeyen terimleri bulabiliriz. Aynı zamanda, çarpma ve bölme işlemlerinin sağlamasını (doğruluğunu kontrol etme) yapabiliriz.
Örnek 3: __ x 9 = 108 işleminde verilmeyen çarpanı bulalım.
108 ÷ 9 = 12
- Çarpma işleminde verilmeyen çarpanı bulmak için çarpımı verilen çarpana böleriz. Aynı işlemi yaparak bir çarpma işleminin doğruluğunu da kontrol edebiliriz.
çarpım ÷ 1. çarpan = 2. çarpan
çarpım ÷ 2. çarpan = 1. çarpan
Örnek 4: __ ÷ 14 = 36 işleminde verilmeyen bölüneni bulalım.
36 x 14 = 504
- Bölme işleminde verilmeyen bölüneni bulmak için bölüm ile bölen çarpılır. Kalan varsa çarpıma eklenir. Aynı işlemleri yaparak bir bölme işleminin doğruluğunu da kontrol edebiliriz.
Kalansız Bölme İşlemi → bölüm x bölen = bölünen
Kalanlı Bölme İşlemi → (bölüm x bölen) + kalan = bölünen
Örnek 5: 192 ÷ __ = 8 işleminde verilmeyen böleni bulalım.
192 ÷ 8 = 24
- Bölme işleminde verilmeyen böleni bulmak için bölünen, bölüme bölünür. Kalan varsa önce bölünenden çıkarılır.
Kalansız Bölme İşlemi → bölünen ÷ bölüm = bölen
Kalanlı Bölme İşlemi → (bölünen ÷ bölüm ) + kalan = bölen
Örnek 6: Aşağıda verilen bölme işlemleri ile çarpma işlemleri arasındaki ilişkiyi inceleyelim.

Örnek 7: Aşağıda verilen kalanlı bölme işlemlerinin sağlamasını yapalım.
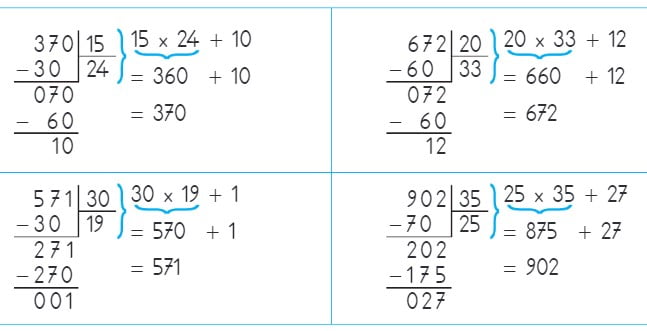
Örnek 8: Aşağıda verilen bölme işlemlerinin bölünenlerini bulalım.

4. Sınıf Çarpma ve Bölme Arasındaki İlişki Çalışma Kağıdı ve Etkinlikleri
Soru: Aşağıdaki kutulara çarpma ve bölme arasındaki ilişkiye göre uygun sayıları yazalım.
| 7 × 3 = 21 | 21 ÷ 7 = __ | __ × 6 = 30 |
| __ ÷ 7 = 3 | 21 ÷ 3 = __ | 30 ÷ __ = 5 |
| 36 ÷ 9 = __ | 36 ÷ 4 = __ | __ ÷ 10 = 7 |
| __ × 9 = 36 | 36 ÷ 9 = __ | 50 ÷ __ = 10 |
| __ × 6 = 30 | 30 ÷ 5 = __ | 8 × __ = 72 |
| 30 ÷ __ = 6 | __ ÷ 6 = 30 | 72 ÷ __ = 9 |
| 8 × 9 = __ | __ ÷ 8 = 9 | 15 × __ = 60 |
| __ ÷ 9 = 8 | 72 ÷ __ = 9 | 60 ÷ 15 = __ |
| 15 × __ = 75 | 75 ÷ 15 = __ | 12 ÷ 4 = __ |
Soru: Aşağıdaki çarpma işlemlerinde verilmeyen çarpanları bölme işlemi yaparak bulalım.
| ………. × 7 = 602 | ………. × 9 = 522 |
| 12 × ………. = 216 | 37 × ………. = 925 |
| ………. × 45 = 540 | ………. × 22 = 880 |
| ………. × 3 = 1245 | ………. × 9 = 2304 |
Soru: Aşağıdaki tabloda verilmeyen terimleri bularak boş kutulara yazalım.
| Bölünen | Bölen | Bölüm | Kalan |
|---|---|---|---|
| 15 | 18 | 7 | |
| 765 | 17 | ||
| 133 | 16 | 5 | |
| 825 | 25 | 33 | 0 |
| 106 | 8 | 2 | |
| 35 | 16 | 10 |
Soru: Aşağıdaki işlemlerde bölünen sayıyı bulmak için bölen ile bölümü çarpınız.
| Bölme İşlemi | Çarpma İşlemi |
|---|---|
| ……… ÷ 12 = 57 | 57 x 12 = 684 |
| ……… ÷ 18 = 26 | ……… x ……… = ……… |
| ……… ÷ 15 = 16 | ……… x ……… = ……… |
| ……… ÷ 13 = 24 | ……… x ……… = ……… |
| ……… ÷ 11 = 45 | ……… x ……… = ……… |
| ……… ÷ 14 = 61 | ……… x ……… = ……… |
| ……… ÷ 9 = 253 | ……… x ……… = ……… |
| ……… ÷ 3 = 574 | ……… x ……… = ……… |
| ……… ÷ 13 = 67 | ……… x ……… = ……… |
Çarpma ve Bölme Arasındaki İlişki Video
4. Sınıf Çarpma ve Bölme Arasındaki İlişki Konu anlatımı, etkinlikleri
- Çarpma ve Bölmenin Temel Kavramları:
- Çarpma: Belirli bir sayının belirli bir sayıda tekrarlanarak toplanmasıdır. Örneğin, 4 x 5 = 20, 4'ün 5 kez tekrarlanarak toplanmasıdır.
- Bölme: Belirli bir sayının eşit parçalara ayrılmasıdır. Örneğin, 20 ÷ 4 = 5, 20'nin 4 eşit parçaya bölünmesi anlamına gelir.
- Çarpma ve Bölme Arasındaki İlişki:
- Çarpma ve bölme işlemleri birbirlerinin tersidir. Bir çarpma işleminin sonucu, bölme işlemiyle doğrulanabilir. Örneğin, 3 x 4 = 12 işlemi, 12 ÷ 4 = 3 veya 12 ÷ 3 = 4 bölme işlemleriyle kontrol edilebilir.
- Herhangi bir çarpma işlemi, ilgili bölme işlemleriyle kontrol edilebilir. Örneğin, 6 x 7 = 42 ise, 42 ÷ 6 = 7 ve 42 ÷ 7 = 6 işlemleri doğru olmalıdır.
- Problem Çözme Stratejileri:
- Çarpma kullanarak bölme problemi çözme: Bir bölme problemini çözmek için bazen çarpma işlemi kullanmak faydalıdır. Örneğin, 24 ÷ 6 = ? sorusu, 6 ile hangi sayıyı çarptığımızda 24 elde ederiz? diye düşünüldüğünde, cevap 4'tür.
- Bölme kullanarak çarpma problemi kontrol etme: Bir çarpma problemini bölme işlemi ile kontrol edebilirsiniz. Örneğin, 8 x 5 = 40 ise, 40 ÷ 5 = 8 ve 40 ÷ 8 = 5 olmalıdır.





