Kaldırma kuvveti, bir sıvı veya gaz içinde bulunan bir cismin üzerine etki eden yukarı yönlü kuvvettir. Bu kuvvet, bir cismin batma veya yüzme davranışını belirler ve Archimedes Prensibi ile açıklanır. Archimedes Prensibi, bir cismin batırıldığı sıvının ağırlığına eşit bir kaldırma kuvveti tarafından yukarı itildiğini belirtir. Kaldırma kuvveti, birkaç önemli değişkene bağlıdır: sıvının yoğunluğu, cismin hacmi ve yerçekimi ivmesi. Bu makalede, kaldırma kuvvetinin bağlı olduğu bu değişkenler detaylı bir şekilde ele alınacaktır.

Su yüzeyine konulan bir tahta parçası batmaz. Bu durum, cismin yoğunluğunun suyun yoğunluğundan düşük olmasıyla ilgilidir. Aynı şekilde, gaz dolu bir balon da havada yükselir, çünkü havadan daha az yoğun bir gazla doludur. Durgun sıvılar ve gazlar, içinde bulundukları cisimlere kaldırma kuvveti uygular. Sıvılar ve gazlar, temas ettikleri cisimlere basınç uygularlar ve bu basınç cisimlerin her yüzeyine etki eder. Özellikle, alt yüzeye uygulanan basınç üst yüzeye uygulanan basınçtan daha büyüktür, bu da cismi yukarı doğru iter.

Bu yukarı itme kuvvetine kaldırma kuvveti denir. Kaldırma kuvveti, cismin sıvı içindeki tüm yüzeylerine etki eden sıvı basıncının vektörel toplamıdır.

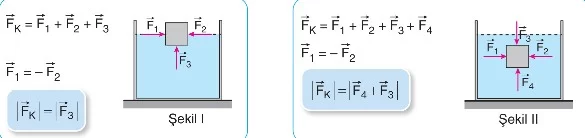
• Şekil I: Cisim su yüzeyinde yüzüyorsa, alt yüzeye sıvının uyguladığı basınç kuvveti daha büyüktür, bu yüzden cisim yukarı doğru kaldırılır. Üst yüzeydeki sıvı basıncı daha düşük olduğu için bu kuvvet farkı cismi yukarı iter.

  Formül:

  $$F_{k} = F_{1} + F_{2} + F_{3} \quad \text{ve} \quad F_{1} = – F_{2}$$Bu durumda:

  $$F_{k} = F_{3}$$

• Şekil II: Cisim tamamen sıvının içindeyse, tüm yüzeylerine sıvı tarafından basınç uygulanır. Alt yüzeydeki basınç yine üst yüzeydeki basınçtan daha büyüktür, dolayısıyla kaldırma kuvveti cismin batmasını engeller.

  Formül:

  $$F_{k} = F_{1} + F_{2} + F_{3} + F_{4}$$ve:

  $$F_{1} = – F_{2}, \quad F_{k} = F_{4} – F_{3}$$

Sonuç olarak, cisim yüzeyde de bulunsa, tamamen sıvının içinde de olsa, kaldırma kuvveti her zaman sıvının cisme uyguladığı basınç kuvvetlerinden doğar. Kaldırma kuvveti cismin yoğunluğu ile sıvının yoğunluğu arasındaki farkla ilişkilidir. Cismin yoğunluğu sıvıdan küçükse, cisim yüzeye çıkar ve yüzer; yoğunluğu büyükse batar.

1. Yüzme Durumu

Bir cismin bir kısmı sıvının içinde, diğer kısmı ise sıvının dışında kalacak şekilde dengede kalmasına yüzme durumu denir. Bu durumda, kaldırma kuvvetinin büyüklüğü cismin ağırlığına eşittir.

$$F_{k} = G$$

Yani:

$$V_{batan} \cdot d_{sıvı} \cdot g = V_{cisim} \cdot d_{cisim} \cdot g$$

Bu denkleme göre, cismin hacmi, batan hacimden büyükse cisim yüzer ve kaldırma kuvveti cismi dengede tutar.

Temel Özellikler:

• Cismin hacmi, batan hacimden büyüktür.
• Sıvının özkütlesi, cismin özkütlesinden büyükse cisim yüzer.
• Kaldırma kuvveti, cisim üzerine etki eden sıvının ağırlığı ile doğru orantılıdır.
• Aynı sıvıda yüzen iki cisimden batma miktarı fazla olan cisme daha fazla kaldırma kuvveti uygulanır.

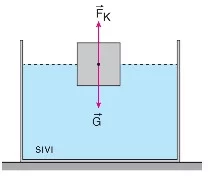
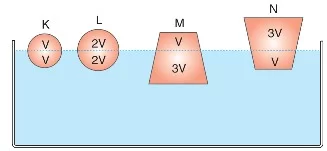
• K ve L cisimlerinin batma oranları eşittir ve her ikisine de aynı büyüklükte kaldırma kuvveti uygulanır.
• M cismi ise K ve L’ye göre daha fazla batmıştır, dolayısıyla en büyük kaldırma kuvveti ona uygulanır.
• Cisimlerin batma oranları, özkütleleri ile ilişkilidir. M cisminin özkütlesi K ve L‘den büyüktür.

Batma Miktarı ve Kaldırma Kuvveti:

• Cisimler arasında en fazla batan M cismine, en büyük kaldırma kuvveti uygulanır.
• Cisimlerin hacimleri eşit olduğunda, özkütlesi en fazla olan cisim daha çok batar.
• Yani d_M > d_K = d_L > d_N.

Bu şekilde, kaldırma kuvveti ile batma miktarı arasındaki ilişki anlaşılabilir ve sıvı içindeki cisimlerin dengesi sağlanır.

Askıda Kalma Durumu

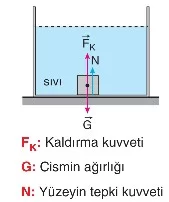
Bir cisim sıvı içine bırakıldığında, eğer kabın tabanına değmeden dengede kalıyorsa bu duruma askıda kalma durumu denir. Askıda kalan cisim hareketsiz kalır çünkü kaldırma kuvveti cismin ağırlığına eşittir. Bu durumda cisim üzerinde iki kuvvet dengededir:

$$F_k = G$$

Burada:

• Fₖ: Kaldırma kuvveti (N),
• G: Cismin ağırlığı (N).

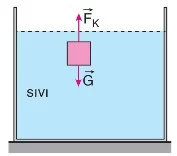
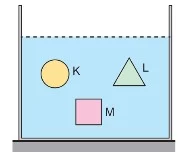
Kaldırma kuvveti cismin yer değiştirdiği sıvının hacmi, sıvının özkütlesi ve yer çekimi ivmesine bağlıdır. Ağırlık ise cismin hacmi, cismin özkütlesi ve yerçekimi ivmesine bağlıdır.

$$V_{batan} \cdot d_{sıvı} \cdot g = V_{cisim} \cdot d_{cisim} \cdot g$$

Burada:

• Vₑ: Batan hacim (m³),
• dₛ: Sıvının özkütlesi (kg/m³),
• g: Yerçekimi ivmesi (m/s²),
• Vᶜ: Cismin hacmi (m³),
• dₐ: Cismin özkütlesi (kg/m³).

Askıda kalma durumunda:

$$V_{batan} = V_{cisim}$$ $$d_{cisim} = d_{sıvı}$$

Yani, askıda kalma durumunda cisim, sıvı ile aynı özkütleye sahiptir. Bu nedenle sıvı içinde ne tamamen batar ne de yüzeye çıkar, dengede kalır.

Batma Durumu

Bir cisim sıvı yüzeyine serbest bırakıldığında, eğer cismin ağırlığı (G) kaldırma kuvvetinden (Fₖ) büyükse, cisim sıvının içine batmaya başlar ve kabın tabanına inerek dengede kalır. Bu duruma batma durumu denir.

Bu durumda aşağıdaki eşitsizlik geçerlidir:

$$G = F_k + N$$
$$G > F_k$$ $$d_{cisim} > d_{sıvı}$$

Burada:

• G: Cismin ağırlığı (N),
• Fₖ: Kaldırma kuvveti (N),
• N: Cismin kabın tabanına uyguladığı normal kuvvet (N),
• dₐ: Cismin özkütlesi,
• dₛ: Sıvının özkütlesi.

• Eğer cisim, sıvının kaldırma kuvvetinin yetersiz kalması sonucu sıvı içinde tamamen batar ve kabın tabanına oturursa, cismin özkütlesi sıvının özkütlesinden büyüktür.
• Cisim tamamen batarsa, sıvının cisme uyguladığı kaldırma kuvveti, cismin ağırlığından küçük olur.

Örnek:

İçi boş olmayan bir çelik parçası, çelik malzemenin yoğunluğu suyun yoğunluğundan büyük olduğu için batacaktır. Ancak içi boşluklu olarak inşa edilen gemiler, çelik kullanılsa bile suyun üzerinde kalır. Bunun nedeni, geminin genel yoğunluğunun suyun yoğunluğundan küçük olacak şekilde tasarlanmış olmasıdır. Bu sayede, gemiler tonlarca ağırlıkta olsalar bile su üzerinde yüzebilir.

Birbirine Karışmayan Sıvıların Kaldırma Kuvveti

Birbirine karışmayan sıvılar içinde dengede olan cisimlere, her sıvı ayrı ayrı kaldırma kuvveti uygular. Özkütlesi farklı olan iki sıvı, içinde bulundukları cisme iki farklı kaldırma kuvveti uygular. Bu sıvılar içinde yüzdürülen bir cisim, bu sıvılardan ayrı ayrı kaldırma kuvveti alır.

Örneğin, d₁ özkütleli sıvı ve d₂ özkütleli sıvılarda bulunan bir cisim, sıvıların hacimlerine göre kaldırma kuvveti alır. Bu durumda:

$$|F_1 + F_2| = G_{cisim}$$

Yani:

$$V_1 \cdot d_1 \cdot g + V_2 \cdot d_2 \cdot g = V_{cisim} \cdot d_{cisim} \cdot g$$

Burada:

• V₁, V₂: Cisme batan kısımlarının hacmi (m³),
• d₁, d₂: Sıvıların özkütlesi (kg/m³),
• g: Yerçekimi ivmesi (m/s²),
• V_cisim: Cismin hacmi (m³),
• d_cisim: Cismin özkütlesi (kg/m³).

Cisimlerin Havadaki ve Sıvıdaki Ağırlıkları

Bir cismin hava ortamındaki ağırlığı, dinamometrede D₁ = G (yani cismin gerçek ağırlığı) ile gösterilir. Ancak cisim sıvı içerisine daldırıldığında, dinamometrenin gösterdiği değer azalır. Bunun nedeni sıvının cisme uyguladığı kaldırma kuvvetidir.

Dinamometredeki gösterilen ağırlık şu formülle hesaplanır:

$$G = F_k + D_2$$

Burada:

• G: Cismin ağırlığı,
• Fₖ: Sıvının cisme uyguladığı kaldırma kuvveti,
• D₂: Sıvı içindeki ağırlık (dinamometrenin gösterdiği değer).

Eğer cisim ip ile alttan bağlanarak batırılırsa, dinamometre ip gerilimini ve kaldırma kuvvetini ölçer. Bu durumda:

$$F_k = T_{ip} + G$$

Bu formüle göre kaldırma kuvveti, ip gerilimi ve cismin ağırlığının toplamına eşit olur.

Sıvı İçindeki Esnek Cisimlere Uygulanan Kaldırma Kuvveti

Sıvı içinde bulunan esnek cisimlerin üzerine uygulanan basınç, cismin hacminin artmasına veya azalmasına neden olabilir. Bu durumda, cisme etki eden kaldırma kuvveti değişir. Esnek cisimlerin hacmi sıvı basıncına bağlı olarak artabilir veya küçülebilir, dolayısıyla kaldırma kuvveti de bu değişime göre farklılık gösterir.

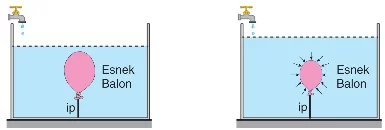
• Sıvı Eklendiğinde: Bir kaba sıvı eklendiğinde, balon üzerindeki sıvı yüksekliği artar. Artan sıvı basıncı nedeniyle balona uygulanan dış basınç artar ve balonun hacmi küçülür. Bu durumda balonun hacmi küçüldüğü için, balona etki eden kaldırma kuvveti azalır.
• Sıvı Seviyesi Azaldığında: Musluk açılıp kap içindeki sıvı seviyesi azaldığında, balon üzerindeki sıvı basıncı azalır. Böylece balonun üzerindeki basınç azalır ve balonun hacmi artar. Hacmi artan balona uygulanan kaldırma kuvveti de artar.

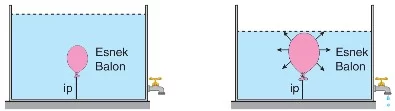
Bu durumda, esnek cisimlerin sıvı içinde davranışı, üzerine uygulanan sıvı basıncının değişmesiyle kaldırma kuvvetinin değişmesine yol açar. Bu, cisimlerin hacmindeki artış veya azalma ile ip geriliminin artmasına veya azalmasına da neden olabilir.

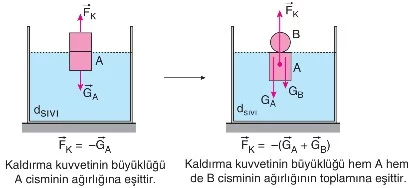
Bir sıvı içinde yüzen katı A cismine uygulanan kaldırma kuvveti, cismin ağırlığına eşittir. Yani, cisim dengede olduğu için kaldırma kuvveti ile ağırlık birbirine eşittir.

Eğer katı A cismi üzerine katı B cismi yerleştirilir ve her iki cisim de sıvı içinde yüzmeye devam ederse, A ve B cisimlerinin toplam ağırlığı, sıvının cisimlere uyguladığı kaldırma kuvvetinin büyüklüğüne eşit olur.

Bu durumda, sıvı her iki cismin toplam ağırlığını dengelemek için toplam kaldırma kuvveti sağlar.

Archimedes Prensibi

Archimedes Prensibi, bir sıvı veya gaz içinde bulunan bir cismin, yer değiştirdiği sıvının ağırlığına eşit bir kaldırma kuvvetine maruz kaldığını belirtir. Kaldırma kuvveti (F_b​) şu formülle ifade edilir:

F_b ​= ρVg

Burada ρ sıvının yoğunluğu, $V$ cismin batırılan hacmi ve g yerçekimi ivmesidir. Bu formül, kaldırma kuvvetinin sıvının yoğunluğu, cismin hacmi ve yerçekimi ivmesi gibi faktörlere bağlı olduğunu gösterir.

Sıvının Yoğunluğu ($\rho$)

Sıvının yoğunluğu, kaldırma kuvvetinin büyüklüğünü belirleyen en önemli faktörlerden biridir. Yoğunluk, birim hacimdeki kütle miktarını ifade eder ve genellikle kilogram/metreküp (kg/m³) birimiyle ölçülür. Daha yoğun sıvılar, daha büyük bir kaldırma kuvveti oluşturur.

Örnek:

• Tatlı suyun yoğunluğu yaklaşık 1000 kg/m³ iken, tuzlu suyun yoğunluğu daha yüksektir. Bu nedenle, tuzlu suda yüzen bir cisim, tatlı suya göre daha büyük bir kaldırma kuvvetine maruz kalır ve daha kolay yüzer.

Cismin Hacmi ($V$)

Cismin batırılan hacmi, kaldırma kuvvetinin büyüklüğünü belirleyen diğer bir önemli faktördür. Cismin hacmi ne kadar büyükse, yer değiştirdiği sıvının hacmi ve dolayısıyla kaldırma kuvveti de o kadar büyük olur. Yüzen bir cismin sadece suya batırılan kısmı, kaldırma kuvvetini belirler.

Örnek:

• Büyük bir gemi, büyük bir hacme sahip olduğu için suya batırılan kısmı da büyüktür ve bu nedenle büyük bir kaldırma kuvvetine maruz kalır. Bu kuvvet, geminin su yüzeyinde kalmasını sağlar.

Yerçekimi İvmesi ($g$)

Yerçekimi ivmesi, kaldırma kuvvetinin büyüklüğünü etkileyen bir diğer faktördür. Yerçekimi ivmesi, bir cismin yerçekimi etkisiyle kazandığı hızlanmayı ifade eder ve genellikle yaklaşık 9.81 m/s² olarak kabul edilir. Yerçekimi ivmesi, kaldırma kuvvetinin formülünde doğrudan yer alır ve cismin maruz kaldığı kaldırma kuvvetini artırır.

Örnek:

• Dünya’daki yerçekimi ivmesi, Ay’daki yerçekimi ivmesinden daha büyüktür. Bu nedenle, aynı sıvı içinde bulunan bir cisim, Dünya’da Ay’a göre daha büyük bir kaldırma kuvvetine maruz kalır.

Günlük Yaşamda Kaldırma Kuvveti

Kaldırma kuvveti, günlük yaşamda birçok uygulamada karşımıza çıkar. Bu kuvvet, su altı faaliyetlerinde, gemi yapımında ve balonların yükselmesinde önemli bir rol oynar.

Gemiler:

• Gemilerin su yüzeyinde kalması, büyük hacimleri ve suyun yoğunluğu sayesinde büyük kaldırma kuvvetlerine maruz kalmalarıyla sağlanır. Gemi yapımında, geminin ağırlığına karşılık gelen kaldırma kuvvetinin hesaplanması hayati önem taşır.

Balonlar:

• Helyum gazı ile doldurulan balonlar, havadan daha düşük yoğunluğa sahip oldukları için yükselirler. Helyum gazının yoğunluğu havadan düşük olduğundan, balonlar yukarı doğru bir kaldırma kuvvetine maruz kalır ve yükselirler.

Dalgıçlar:

• Dalgıçlar, su altında belirli bir derinlikte kalmak veya yüzeye çıkmak için ağırlık kemerleri ve yüzerlik yelekleri kullanırlar. Bu ekipmanlar, dalgıcın su altındaki kaldırma kuvvetini dengelemeye yardımcı olur.

Kaldırma kuvveti, bir cismin batırıldığı sıvının yoğunluğu, cismin hacmi ve yerçekimi ivmesi gibi faktörlere bağlıdır. Bu faktörler, cismin sıvı içinde batma veya yüzme davranışını belirler. Archimedes Prensibi, kaldırma kuvvetinin temelini oluşturur ve bu prensip günlük yaşamda birçok alanda uygulanır. 9. sınıf fizik dersinde kaldırma kuvvetinin bağlı olduğu değişkenlerin öğrenilmesi, öğrencilerin bu kavramı anlamalarına ve çeşitli problemleri çözme becerilerini geliştirmelerine yardımcı olur.