10. Sınıf Matematik Konu Anlatımı
1. Ünite: Sayma ve Olasılık
- Sıralama ve Seçme
– Sayma Yöntemleri (Toplama ve Çarpma Yoluyla Sayma)
– Faktöriyel
– Permütasyon
– Tekrarlı Permütasyon
– Kombinasyon
– Pascal Üçgeni
– Binom Açılımı - Basit Olayların Olasılıkları
2. Ünite: Fonksiyonlar
- Fonksiyon Kavramı ve Gösterimi
– Fonksiyon Kavramı, Tanımı, Gösterimi
– Fonksiyon Çeşitleri (Parçalı Fonksiyon, Birim Fonksiyon, Sabit Fonksiyon, Doğrusal Fonksiyon, Eşit Fonksiyonlar, Tek ve Çift Fonksiyon, Bire Bir Fonksiyon, Örten ve İçine Fonksiyon)
– Fonksiyonlarda Dört İşlem
– Fonksiyon Grafikleri (Doğrusal Fonksiyonların Grafikleri, Parçalı Fonksiyonların Grafikleri, Yatay ve Dikey Doğru Testi, Grafikler ile İlgili Problemler) - İki Fonksiyonun Bileşkesi ve Bir Fonksiyonun Tersi
– Fonksiyonlarda Bileşke İşlemi
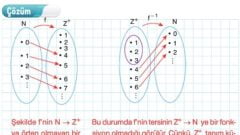
– Ters Fonksiyonlar ve Grafikleri
3. Ünite: Polinomlar
- Polinom Kavramı ve Polinomlarla İşlemler
– Polinom Kavramı
– Polinomlarla Dört İşlem - Polinomların Çarpanlara Ayrılması
– Ortak Çarpan Parantezine Alarak Çarpanlara Ayırma
– Gruplandırarak Çarpanlara Ayırma
– Tam Kare Özdeşliğini Kullanarak Çarpanlara Ayırma
– İki Kare Farkı Özdeşliğini Kullanarak Çarpanlara Ayırma
– İki Terimin Toplamının ve Farkının Küpü Özdeşliğini Kullanarak Çarpanlara Ayırma
– İki Terimin Küpünün Toplamı ve Farkı Özdeşliğini Kullanarak Çarpanlara Ayırma
– x2+ bx + c ve ax2+ bx + c Şeklindeki Üç Terimlilerin Çarpanlarına Ayrılması
– Değişken Değiştirme Yöntemi ile Çarpanlara Ayırma
– Rasyonel İfadeler
4. Ünite: İkinci Dereceden Denklemler
- İkinci Dereceden Bir Bilinmeyenli Denklemlerin Çözümü
- İkinci Dereceden Bir Bilinmeyenli Denklemlerin Köklerinin Varlığı ve Diskriminantı
- Karmaşık Sayılar
- İkinci Dereceden Bir Denklemin Kökleri ile Katsayıları Arasındaki İlişki
- Kökleri Verilen İkinci Dereceden Denklemin Yazılması
5. Ünite: Dörtgenler ve Çokgenler
- Çokgenler
- Dörtgenler ve Özellikleri
- Özel Dörtgenler
– Yamuk ve Yamukta Alan
– Paralelkenar ve Paralelkenarda Alan
– Eşkenar Dörtgen ve Eşkenar Dörtgende Alan
– Dikdörtgen ve Paralelkenarda Alan
– Kare ve Karede Alan
– Deltoid ve Deltoidde Alan
6. Ünite: Katı Cisimler
- Dik Prizma
- Dik Piramit
10. Sınıf Matematik Konu Anlatımı, Konu Özeti, Çözümlü Sorular
Soru: Bir zarın 1’den 6’ya kadar olan sayılarla geldiği bir oyunu düşünün. 3 kez zar atılıyor. En az bir kez 5 gelme olasılığı nedir?
Çözüm: Bu tür bir olasılık sorusu için olumsuz durumu hesaplamak ve sonra bu olumsuz durumu olasılıktan çıkarmak daha kolaydır. Olumsuz durum, hiç 5 gelmemesi durumudur ve bu durumu hesaplamak için tüm 3 atışta 5 gelmemesi olasılığını hesaplayabiliriz.
Zarın her atışta 5 gelmemesi olasılığı 5/6’dır (çünkü 5 gelme olasılığı 1/6’dır, bu nedenle gelmeme olasılığı 5/6’dır).
Hiç 5 gelmemesi olasılığını hesaplamak için bu olasılıkları çarparız: (5/6) * (5/6) * (5/6) = 125/216
Şimdi bu olumsuz durumu hesapladık. Şimdi, bu olumsuz durumu toplam olasılıktan çıkararak en az bir kez 5 gelme olasılığını hesaplayabiliriz:
1 – 125/216 = 91/216
Bu nedenle, en az bir kez 5 gelme olasılığı 91/216’dır.
Soru: F(x) = 2x – 3 ve g(x) = x^2 + 4x – 1 fonksiyonları verilmiştir. F(g(2)) ifadesini hesaplayın.
Çözüm: Bu tür bir soruyu çözmek için, önce iç içe geçmiş fonksiyonları çözmelisiniz. İlk olarak, g(2)’yi hesaplayalım:
g(x) = x^2 + 4x – 1 g(2) = 2^2 + 4 * 2 – 1 g(2) = 4 + 8 – 1 g(2) = 11
Şimdi, g(2) sonucunu kullanarak F(g(2))’yi hesaplayabiliriz:
F(x) = 2x – 3 F(g(2)) = 2 * 11 – 3 F(g(2)) = 22 – 3 F(g(2)) = 19
Sonuç olarak, F(g(2)) ifadesinin değeri 19’dur.
Soru: P(x) = 2x^3 – 3x^2 + 4x – 1 ve Q(x) = x^2 – 2x + 1 polinomları verilmiştir. P(x) ve Q(x) polinomlarını toplayın.
Çözüm: Polinomları toplamak için ilgili terimleri bir araya getiririz. Verilen polinomlar şunlardır:
P(x) = 2x^3 – 3x^2 + 4x – 1 Q(x) = x^2 – 2x + 1
Şimdi bu iki polinomu toplayalım:
P(x) + Q(x) = (2x^3 – 3x^2 + 4x – 1) + (x^2 – 2x + 1)
Şimdi aynı dereceden terimleri gruplayarak toplama işlemini yapalım:
P(x) + Q(x) = 2x^3 + (x^2 – 3x^2) + (4x – 2x) + (-1 + 1)
Şimdi terimleri toplayarak sonucu elde edelim:
P(x) + Q(x) = 2x^3 – 2x^2 + 2x
Sonuç olarak, P(x) ve Q(x) polinomlarını topladığınızda elde edilen yeni polinom şu şekildedir:
P(x) + Q(x) = 2x^3 – 2x^2 + 2x
ax^2 + bx + c = 0
Bu tür bir denklemin köklerini (x’in değerlerini) bulmak için aşağıdaki formülü kullanabilirsiniz:
x = (-b ± √(b^2 – 4ac)) / 2a
Şimdi bir örnek ikinci dereceden denklem çözümünü gösterelim:
Soru: 2x^2 – 5x – 3 = 0 ikinci dereceden bir denklemdir. Bu denklemin köklerini bulun.
Çözüm: Verilen denkleme göre, a = 2, b = -5 ve c = -3’dir. Şimdi kökleri hesaplamak için formülü kullanabiliriz:
x = (-(-5) ± √((-5)^2 – 4 * 2 * (-3))) / (2 * 2)
Şimdi bu denklemi çözebiliriz:
x = (5 ± √(25 + 24)) / 4 x = (5 ± √49) / 4 x = (5 ± 7) / 4
Şimdi iki farklı kökü bulduk:
- x = (5 + 7) / 4 = 12 / 4 = 3
- x = (5 – 7) / 4 = -2 / 4 = -1/2
Sonuç olarak, verilen ikinci dereceden denklemin kökleri 3 ve -1/2’dir.
Soru: Bir dikdörtgen prizmanın uzunluğu (L) 10 cm, genişliği (W) 5 cm ve yüksekliği (H) 3 cm’dir. Bu prizmanın hacmini hesaplayın.
Çözüm: Dikdörtgen prizmanın hacmini hesaplamak için hacim formülünü kullanabiliriz:
Hacim (V) = Uzunluk (L) x Genişlik (W) x Yükseklik (H)
Verilen değerleri yerine koyarak hesaplama yapabiliriz:
V = 10 cm x 5 cm x 3 cm
V = 150 cm³
Bu nedenle, bu dikdörtgen prizmanın hacmi 150 cm³’dir.
Dik Prizma Sorusu:
- Bir dik prizmanın yüksekliği 10 cm ve taban alanı 30 cm² ise, prizmanın hacmi nedir?Çözüm: Dik prizmanın hacmi, taban alanının yükseklikle çarpılması ile bulunur. Hacim = Taban Alanı x Yükseklik Hacim = 30 cm² x 10 cm = 300 cm³
Dik Piramit Sorusu: 2. Bir dik piramidin taban kenarının uzunluğu 8 cm ve piramidin yüksekliği 12 cm ise, piramidin hacmi nedir?
Çözüm: Dik piramidin hacmi, piramidin taban alanının yükseklikle çarpılması ve sonucun 1/3 ile çarpılması ile bulunur. Hacim = (Taban Alanı x Yükseklik) / 3 Taban Alanı = 8 cm x 8 cm = 64 cm² Hacim = (64 cm² x 12 cm) / 3 = (768 cm³) / 3 = 256 cm³