4. sınıf matematik müfredatında yer alan “Uzamsal İlişkiler” konusu, öğrencilerin geometrik şekiller ve uzay arasındaki ilişkileri anlamalarını sağlar. Bu bölümde, simetri doğrusu çizme (ayna simetrisi) ve verilen bir şeklin doğruya göre simetriğini çizme gibi konular ele alınacaktır. Simetri kavramı, günlük hayatta sıkça karşılaştığımız bir durumdur ve öğrencilerin bu kavramı anlamaları, çevrelerindeki dünyayı daha iyi kavramalarına yardımcı olur. Bu konular, öğrencilere görsel ve uzamsal düşünme becerileri kazandırarak, geometrik şekillerin özelliklerini ve ilişkilerini keşfetmelerini sağlar.

Simetri Konu Anlatımı

A. Simetri Doğrusu Çizme (Ayna Simetrisi)

Doğrular yardımıyla iki eş parçaya ayrılabilen ve doğrunun bulunduğu çizgiye göre katlandığında birbirinin aynısı olan şekillere simetrik şekiller denir. Simetrik şekillerin uygun yerlerine ayna yerleştirildiğinde, aynanın önündeki görüntü ile aynadaki görüntü, o şekle eştir. Bu tür simetriye “ayna simetrisi“, “aynaya göre simetri” veya “doğruya göre simetri” denir.

Örnek: Aşağıda verilen şekillerin doğruya göre simetrilerini inceleyelim.

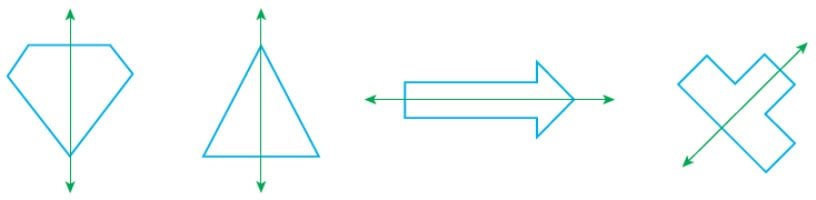
Örnek: Aşağıda verilen geometrik şekillerin simetri doğrularını inceleyelim.

Karenin simetri doğrularını çizelim.

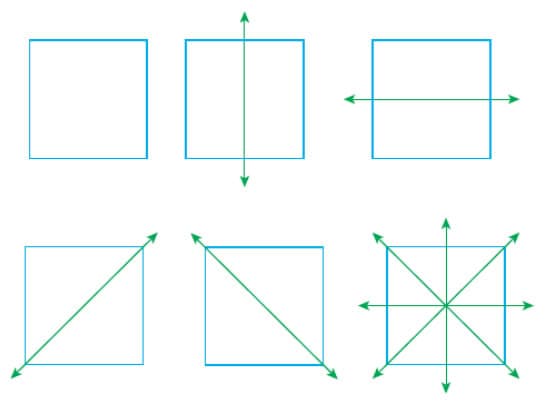
• Karenin 4 tane simetri doğrusu vardır.

Dikdörtgenin simetri doğrularını çizelim.

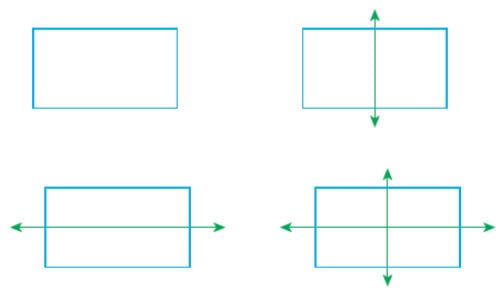
• Dikdörtgenin 2 tane simetri doğrusu vardır.

Not: Bazı şekillerin simetri doğrusu yokken, bazı şekillerin 1’den fazla simetri doğrusu olabilir.

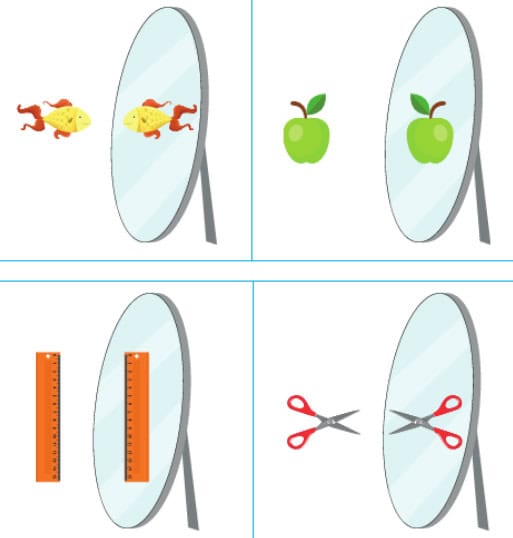
Örnek: Aşağıda aynalarda görüntüleri verilen nesneleri inceleyelim.

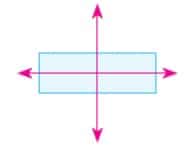
Örnek: Aşağıdakilerden hangisinin simetri doğrusu yanlış çizilmiştir?

Çözüm: Dikdörtgensel şeklin iki simetri doğrusu vardır.

Örnek: Aşağıdakilerden hangisi herhangi bir doğruya göre simetriktir.

B. Verilen Şeklin Doğruya Göre Simetriğini Çizme

• Şekillerin bir doğruya olan uzaklıkları bulunduktan sonra doğrunun diğer tarafından da aynı uzaklık hesaplanarak şekil çizilir.

Örnek: Aşağıda verilen noktaların doğruya göre simetriğini bulalım.

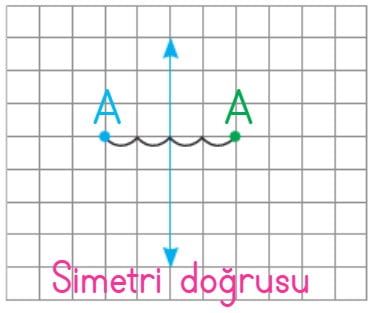
A noktası simetri doğrusuna 2 birim uzaklıktadır. A noktasının simetriği olan A noktası da simetri doğrusuna 2 birim uzaklıktadır.

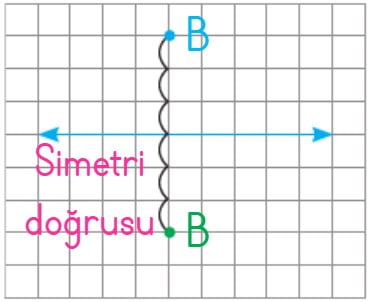
B noktası simetri doğrusuna 3 birim uzaklıktadır. B noktasının simetriği olan B noktası da simetri doğrusuna 3 birim uzaklıktadır.

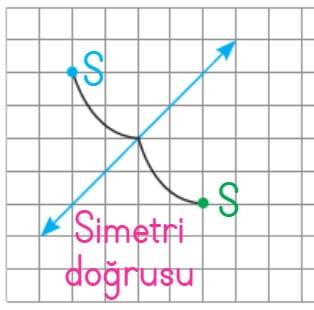
S noktasının simetri doğrusuna olan uzaklığı kadar uzaklık belirlenip aynı hizada S noktası işaretlenir.

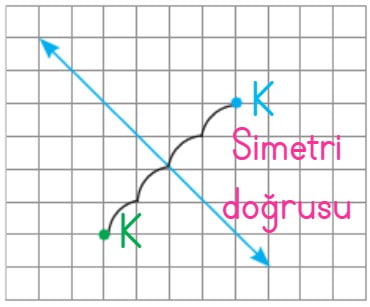
K noktasının simetri doğrusuna olan uzaklığı kadar uzaklık belirlenip aynı hizada K işaretlenir.

Örnek: Aşağıda verilen şekillerin doğruya göre simetriğini bulalım.

Şekil I simetri doğrusuna 2 birim uzaklıktadır. Simetri doğrusunun diğer tarafında 2 birim ilerleyerek şekil II’yi çizdik. Şekil I’in simetriği şekil II’dir.

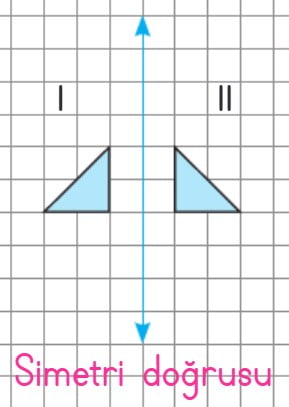
Şekil I simetri doğrusuna 1 birim uzaklıktadır. Simetri doğrusunun diğer tarafında 1 birim ilerleyerek şekil II’yi çizdik. Şekil I’in simetriği şekil II’dir.

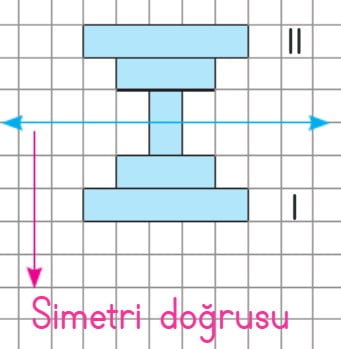
Şekil I şekli simetri doğrusuna bitişiktir. Simetri doğrusuna bitişik olacak şekilde şekil II’yi çizdik. Şekil I’in simetriği şekil II’dir.

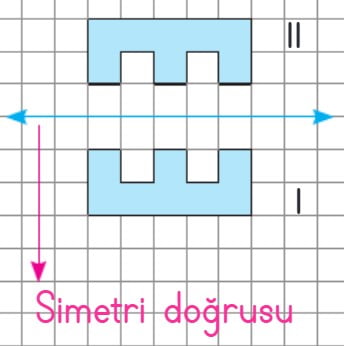
Şekil I simetri doğrusuna 1 birim uzaklıktadır. Simetri doğrusunun diğer tarafında 1 birim ilerleyerek şekil II’yi çizdik. Şekil I’in simetriği şekil II’dir.

Örnek: 

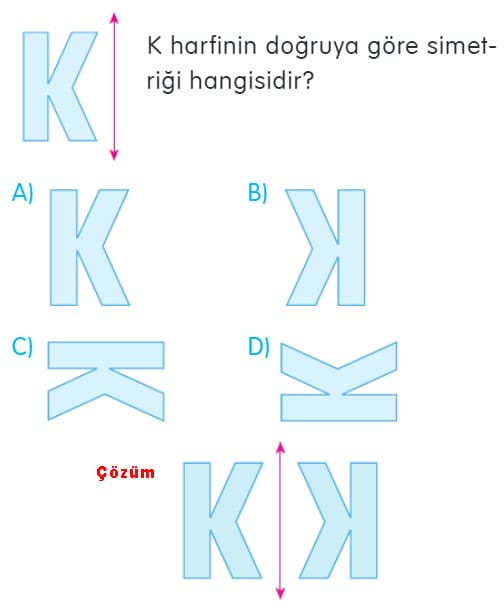
Örnek:

“Yukarıda gösterilen C noktasının simetri doğrusuna göre simetriği hangi noktadadır?
A) A   B) B   C) K   D) L

Çözüm: C noktasının doğruya olan uzaklığı 3 birimdir. Doğrunun diğer tarafında 3 birim uzaklıkta olan nokta B noktasıdır.”

Simetri Çalışma Kağıdı

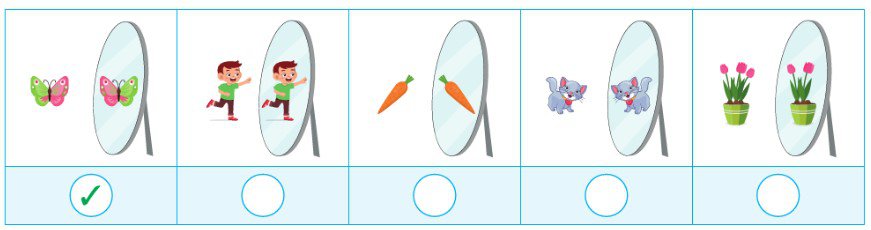
Soru: Aşağıda verilen varlıklardan aynadaki görüntüleri doğru olanları “✓”, doğru olmayanları “✗” işareti ile örnekteki gibi işaretleyiniz.

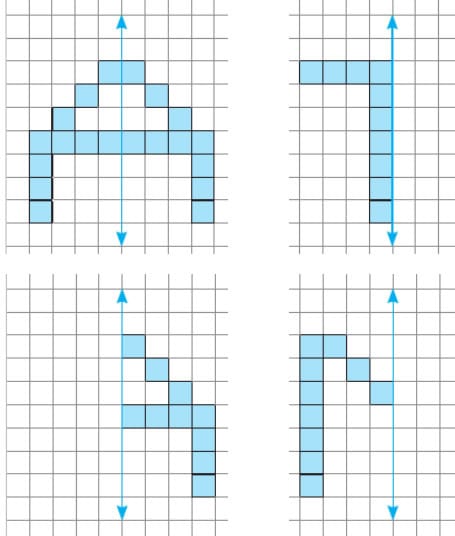
Soru: Aşağıda verilen şekillerin simetri doğrusuna göre simetriğini örnekteki gibi çiziniz.

Soru: Aşağıdaki şekillerden simetrik olanları işaretleyelim. İşaretlediğimiz şekillerin simetri doğrularını çizelim.

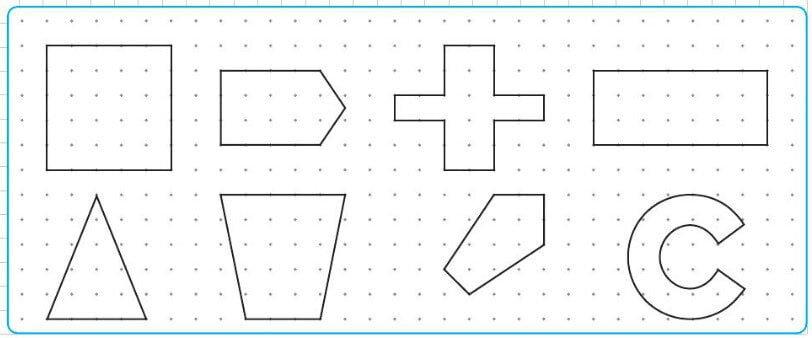
Soru: Aşağıdaki şekillerden simetri doğrularını çizelim.

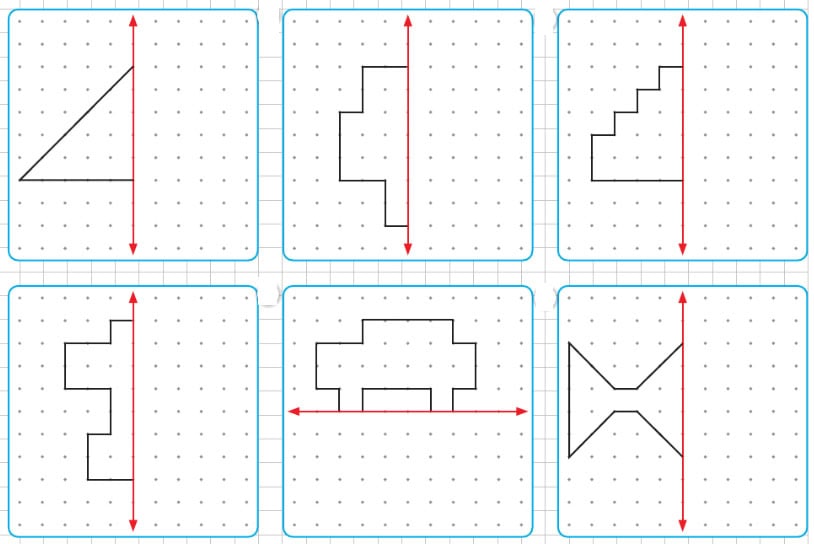
Soru: Aşağıdaki şekillerin verilen simetri doğrusuna göre simetriğini çizelim.

Simetri Video

Simetri Doğrusu Çizme (Ayna Simetrisi)

Simetri, matematikte ve doğada sıkça karşılaştığımız bir kavramdır. Simetri doğrusu, bir şeklin tam ortasından geçen ve şekli iki eş parçaya ayıran hayali bir çizgidir. Bu iki parça, birbirinin ayna görüntüsü gibi görünür. Bir şeklin simetrik olup olmadığını anlamak için simetri doğrusunu kullanırız.

Örneğin, kare gibi bazı şekiller birden fazla simetri doğrusuna sahip olabilir. Bir karede, dikey, yatay ve köşegen olmak üzere dört farklı simetri doğrusu bulunur. Her bir simetri doğrusu, kareyi iki eş ve simetrik parçaya böler. Simetri doğrusu, şekillerin düzenliliğini ve dengeyi anlamamızda önemli bir araçtır.

Verilen Şeklin Doğruya Göre Simetriğini Çizme

Verilen bir şeklin doğruya göre simetriğini çizmek, şeklin aynadaki yansımasını çizmek gibidir. Simetri doğrusu üzerinde bir şeklin diğer tarafındaki yansımasını oluştururken, şeklin her bir noktasının simetri doğrusu üzerinde eşit uzaklıkta yer almasına dikkat ederiz.

Örneğin, bir üçgenin bir simetri doğrusuna göre simetrisini çizmek, üçgenin her bir köşesini simetri doğrusuna eşit uzaklıkta yeni bir köşe ile değiştirmek anlamına gelir. Bu, öğrencilerin uzamsal düşünme becerilerini geliştirmelerine ve şekiller arasındaki ilişkileri daha iyi anlamalarına yardımcı olur.

Simetriyi anlama ve uygulama becerisi, matematiksel düşünme ve görsel algılamayı güçlendirir. Simetri, sadece matematikte değil, sanat, mimari ve doğa gibi pek çok alanda da karşımıza çıkar. Öğrenciler, bu temel kavramları öğrenerek, çevrelerindeki dünyayı daha iyi anlayabilir ve çeşitli problemlere yaratıcı çözümler üretebilirler.