Vektörler 9. Sınıf Fizik

9. Sınıf 9. Sınıf Fizik Konuları Konu Anlatımı

24.09.2024

Fizik, evrendeki olayları anlamak ve açıklamak için matematiksel ve kavramsal araçlar kullanır. Bu araçların en önemlilerinden biri, vektörlerdir. Vektörler, büyüklük ve yön bilgisi içeren fiziksel niceliklerdir ve birçok fiziksel olayı tanımlamak ve analiz etmek için kullanılır. 9. sınıf fizik dersinde vektörlerin yön ve büyüklükleri konusu, öğrencilerin hareket, kuvvet ve diğer vektörel büyüklükleri anlamalarını sağlamak için temel bir konudur.

Vektör Nedir?

Yönü ve büyüklüğü olan doğru parçasına vektör denir. Bir vektörün özellikleri şunlardır:

Başlangıç noktası ve bitiş noktası,
Yönü,
Doğrultusu,
Şiddeti (büyüklüğü, sayısal değeri).

Vektörler, genellikle temsil eden bir harfin üzerine ok işareti ile gösterilir. Örneğin, bir vektörün büyüklüğü |A| veya $\vec{A}$ şeklinde ifade edilir. Aşağıda bir vektörün temel özellikleri gösterilmiştir:

a) Büyüklük (Şiddet)

Bir vektörün büyüklüğü, vektörün uzunluğuyla doğru orantılıdır. Örneğin, $\vec{F}_1$ vektörünün büyüklüğü $|\vec{F}_1| = F_1$ olarak gösterilir.
Eğer ${\vec{F}}_{1} =$ birim, ${\vec{F}}_{2} =$ birim ve ${\vec{F}}_{3} =$ birim ise, vektörlerin büyüklükleri gösterildiği gibi çizilir.

b) Doğrultu

Vektörün doğrultusu, vektörün bulunduğu çizgi üzerinde uzandığı doğrultudur. $\vec{F}_1$ , $\vec{F}_2$ ve $\vec{F}_3$ vektörlerinin doğrultuları doğu-batı doğrultusundadır.

c) Yön

Vektörün yönü, vektörün okunun gösterdiği taraftır. $\vec{F}_1$ ve $\vec{F}_2$ vektörlerinin yönü batı, $\vec{F}_3$ vektörünün yönü doğudur.

d) Başlangıç Noktası

Her vektörün bir başlangıç noktası vardır. Örneğin, $\vec{F}_1$ ‘in başlangıç noktası $O_1$ , $\vec{F}_2$ ‘nin başlangıç noktası $O_2$ , ve $\vec{F}_3$ ‘ün başlangıç noktası $O_3$ ‘dür.

vektörlerine ait büyüklük, yön ve doğrultu özellikleri aşağıda verilmiştir:

$\vec{K}$

$\vec{K}$ ile $\vec{L}$ vektörlerinin yönleri ters, ancak doğrultuları aynıdır. Buna karşın, $\vec{M}$ ile $\vec{N}$ vektörlerinin yön ve doğrultuları birbirinden farklıdır.

Eşit Vektörler

Aynı niceliğe ait, yönleri ve büyüklükleri aynı olan vektörlere eşit vektörler denir.
Örneğin: $\vec{K} = \vec{L}$ ve $\vec{K} = \vec{L}$

Değerleri sayısal olarak aynı olan vektörlerin birimleri farklıysa, vektörler birbirine eşit değildir.
Kuvvet ve hız gibi farklı fiziksel nicelikleri belirten vektörler, büyüklükleri aynı olsa bile birbirine eşit olamaz. Örneğin: Kuvvet $\vec{F} = 10 N$ , hız $\vec{V} = 10 m/s$ olduğunda, $\vec{F} \neq \vec{V}$ olur.

Zıt Vektörler

Aynı niceliğe ait büyüklükleri eşit, aynı doğrultuda, fakat yönleri ters olan vektörlere zıt vektörler denir.
Örneğin: $\vec{X}$ ile $\vec{Y}$ zıt vektörlerdir, $\vec{K}$ ile $\vec{L}$ zıt vektörlerdir.
Formül olarak:
$\vec{X} = -\vec{Y}$ veya $\vec{Y} = -\vec{X}$
$\vec{K} = -\vec{L}$
Zıt vektörlerin büyüklükleri eşit olmalıdır, ancak yönleri birbirine zıttır.

$X$ ile $\vec{Z}$ zıt vektör olmayıp, sadece zıt yönlü vektörlerdir.
Bir vektör, yönü ve büyüklüğü değişmeden aynı düzlemde bir yerden başka bir yere taşınabilir. Bu durumda vektörün özellikleri değişmez.
Şekilde verilen $\vec{K}$ vektörü, farklı yerlere taşınmış olmasına rağmen, doğrultu ve büyüklüğü değişmediği için $\vec{K}$ vektörünün özellikleri de değişmemiştir.

Bir Vektörün Reel Bir Sayıyla Çarpılması

Bir vektör, reel bir sayıyla çarpıldığında yine bir vektör elde edilir. Ancak bu işlem sonucunda vektörün yönü veya büyüklüğü değişebilir, ancak doğrultusu değişmez.

9. Sınıf Vektörler, Vektör Nedir? Özellikleri Konu Anlatımı, Özet

Vektörlerin Tanımı ve Özellikleri

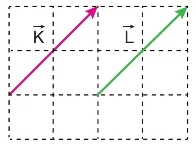
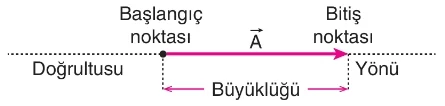
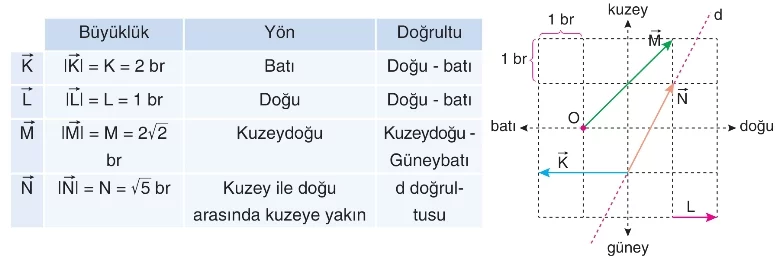
Vektörler, iki temel bileşenden oluşur: büyüklük ve yön. Bir vektörün büyüklüğü, uzunluğu ile temsil edilir ve vektörün ne kadar büyük olduğunu gösterir. Yön ise, vektörün hangi yöne doğru olduğunu ifade eder. Vektörler, genellikle oklarla gösterilir; okun uzunluğu büyüklüğü, oku yönü ise vektörün yönünü belirtir.

Örnekler:

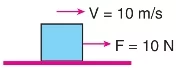
Kuvvet (F): Bir cisme uygulanan kuvvet, hem büyüklük hem de yön içerir. Kuvvetin büyüklüğü, kuvvetin ne kadar güçlü olduğunu; yönü ise, kuvvetin hangi yönde uygulandığını gösterir.
Yer Değiştirme (d): Bir cismin başlangıç noktasından bitiş noktasına olan yönlü mesafe, yer değiştirme vektörü ile ifade edilir. Yer değiştirme, hem alınan yolun miktarını hem de yönünü belirtir.

Vektörlerin Gösterimi

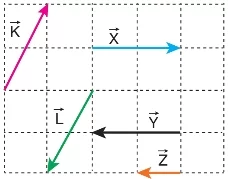
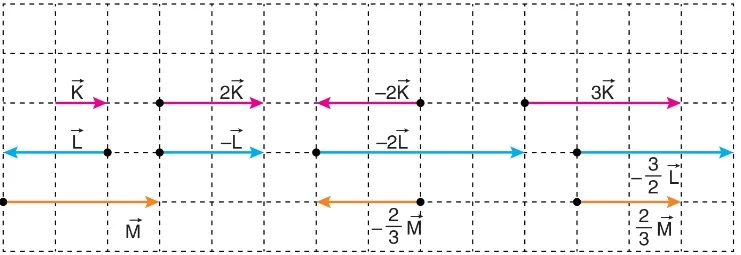
Vektörler, grafiksel olarak ve bileşenleri ile gösterilebilir. Grafiksel gösterimde, vektörler oklar ile temsil edilir. Bileşen gösteriminde ise, bir vektör iki veya daha fazla bileşene ayrılarak ifade edilir.

Grafiksel Gösterim:

Vektörler, başlangıç noktası ve bitiş noktası olan oklar ile çizilir. Örneğin, bir kuvvet vektörü, kuvvetin uygulandığı noktadan başlayıp kuvvetin yönünde uzanan bir ok ile gösterilir.

Bileşen Gösterimi:

Bir vektör, genellikle yatay (x ekseni) ve dikey (y ekseni) bileşenlerine ayrılır. Bu bileşenler, vektörün toplam büyüklüğünü ve yönünü belirlemek için kullanılır. Örneğin, bir yer değiştirme vektörü, yatay ve dikey hareket bileşenlerine ayrılabilir.

Vektörlerin Toplanması ve Çıkarılması

Vektörlerin toplanması ve çıkarılması, fiziksel olayları analiz etmek için sıkça kullanılan işlemlerdir. Vektörlerin toplanması, iki veya daha fazla vektörün bileşenlerinin toplanarak yeni bir vektör elde edilmesi işlemidir. Çıkarma işlemi ise, bir vektörün ters yönlü olarak eklenmesi ile yapılır.

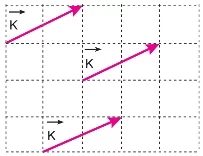
Uç Uca Ekleme Yöntemi:

İki vektör, uç uca eklenerek toplanabilir. Bu yöntemde, birinci vektörün bitiş noktasına ikinci vektörün başlangıç noktası eklenir ve elde edilen yeni vektör, toplam vektörü temsil eder.

Paralel Kenar Yöntemi:

İki vektör, başlangıç noktaları birleştirilerek bir paralel kenar oluşturulur. Paralel kenarın köşegenleri, vektörlerin toplamını gösterir.

Vektörlerin Uygulamaları

Vektörler, birçok fiziksel olayın ve kavramın tanımlanmasında kullanılır. Hareket, kuvvet, hız, ivme gibi büyüklükler vektörel büyüklüklerdir ve vektörler ile analiz edilir.

Hareket:

Bir cismin hareketi, yer değiştirme vektörleri ile tanımlanır. Cismin hangi yöne ve ne kadar mesafe kat ettiğini belirlemek için yer değiştirme vektörleri kullanılır.

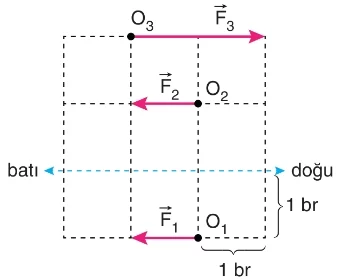
Kuvvet:

Bir cisme etki eden kuvvetler, vektörler ile ifade edilir. Kuvvetlerin bileşenleri, net kuvveti ve dolayısıyla cismin hareketini belirler.

Vektörlerin yön ve büyüklükleri, fiziğin temel konularından biridir ve birçok fiziksel olayı anlamak için gereklidir. 9. sınıf fizik dersinde vektörlerin öğrenilmesi, öğrencilerin bilimsel düşünme ve problem çözme becerilerini geliştirmelerine yardımcı olur. Vektörlerin doğru bir şekilde anlaşılması, öğrencilerin ileri düzey fizik konularını ve günlük yaşamda karşılaştıkları fiziksel olayları daha iyi kavramalarını sağlar.