Birden fazla vektörün etkisini tek başına ifade eden vektöre bileşke vektör ya da toplam vektör denir. Bileşke vektör birkaç yöntemle bulunabilir:

• Uç uca ekleme yöntemi
• Dik bileşenlerine ayırma yöntemi
• Paralelkenar yöntemi

Notlar:

• Vektörel toplama, sayıların toplanmasıyla aynı işlem değildir. Vektörlerin büyüklüklerinin yanı sıra yönleri de dikkate alınarak toplama yapılmalıdır.
• Aynı tür vektörler arasında toplama ve çıkarma işlemleri yapılabilir. Örneğin, bir kuvvet vektörü yalnızca başka bir kuvvet vektörü ile toplanabilir.
• Farklı tür vektörler arasında toplama ve çıkarma işlemi yapılamaz; ancak çarpma işlemi mümkündür.

Uç Uca Ekleme Yöntemi

Vektörler, yönü ve büyüklüğü değişmeden, birinin bitiş noktası diğerinin başlangıç noktasına gelecek şekilde eklenir. İlk vektörün başlangıç noktası ile son vektörün bitiş noktası arasında çizilen vektör, bileşke vektörü oluşturur ve bu vektör genellikle $\vec{R}$ ile gösterilir.

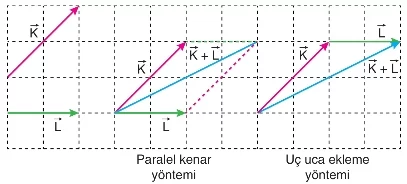
Birimkarelere bölünmüş düzlemde $\vec{K}$, $\vec{L}$ ve $\vec{M}$ vektörleri ile bileşke vektörler $\vec{R}_1 = \vec{M} + \vec{L}$ ve $\vec{R}_2 = \vec{K} + \vec{L} + \vec{M}$ uç uca ekleme yöntemiyle bulunmuştur. Bu yöntemde vektörlerin eklenme sırası önemli değildir.

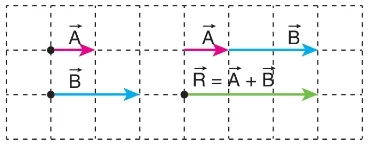
Aynı Doğrultuda Yer Alan Vektörlerin Uç Uca Ekleme Yöntemiyle Toplanması

Şekildeki $\vec{A}$ vektörü ile $\vec{B}$ vektörü aynı yöndedir. Vektörlerin bileşkesi de aynı yönde olur. Bileşke vektörün büyüklüğü, vektörlerin büyüklüklerinin toplamına eşittir.

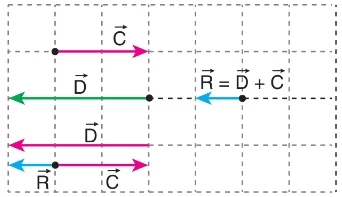
Şekildeki $\vec{C}$ ve $\vec{D}$ vektörleri zıt yönlüdür. Vektörlerin bileşkesinin yönü, büyük olan vektörün yönünde olur. Bileşke vektörün büyüklüğü ise vektörlerin büyüklüklerinin farkına eşittir.

Farklı Doğrultudaki Vektörlerin Uç Uca Ekleme Yöntemiyle Toplanması

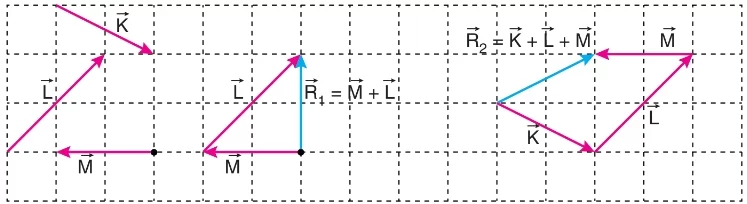
Farklı doğrultulardaki vektörler uç uca eklenerek toplanırken, vektörlerin doğrultuları ve yönleri değiştirilmeden taşınarak bileşke vektör bulunur. Bu yöntemde, bir vektörün okuna diğer vektörün başlangıç noktası eklenir (toplanacak vektörlerin başlangıç noktaları veya okları çakışmamalıdır). Hepsi bu şekilde eklendikten sonra, ilk vektörün başlangıç noktasından son vektörün okuna çizilen vektör, bileşke vektör olarak adlandırılır.

Uç uca eklenen vektörler, kapalı bir bölge oluşturuyorsa bu vektörlerin bileşkesi sıfırdır. Örneğin:
$\vec{K} + \vec{L} + \vec{N} + \vec{M} = 0$

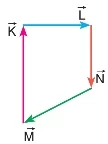
Ancak her kapalı vektör sisteminin bileşkesi sıfır olmayabilir. Uç uca eklenip eklenmediğine dikkat edilmelidir. Şekildeki gibi eklenen $\vec{F}_1$, $\vec{F}_2$, $\vec{F}_3$ vektörlerinin bileşkesi sıfır değildir.

Vektörlerde Çıkarma İşlemi

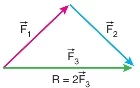
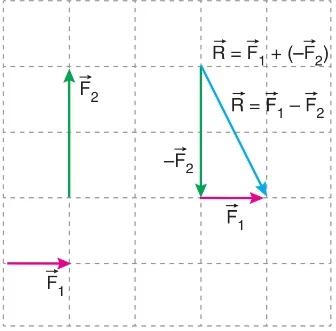
İki vektörün çıkarılması, aslında bir vektörel toplama işlemidir. Çıkarılacak olan vektörün yönü ters çevrilip, diğer vektörle toplanır. Örneğin, $\vec{F}_1 – \vec{F}_2$ işlemi yapılırken, $\vec{F}_2$ vektörünün yönü ters çevrilir ve $\vec{F}_1$ ile toplanır.

Örneğin, şekil üzerinde $\vec{F}_1$ ve $\vec{F}_2$ vektörleri arasındaki $\vec{F}_1 – \vec{F}_2$işlemi yapılırken, $\vec{F}_2$ vektörünün yönü ters çevrilir. Ardından $\vec{F}_1$ vektörünün başlangıç noktası ile $\vec{F}_2$‘nin ters yönlendirilmiş hali uç uca eklenir. Sonuçta, başlangıç noktası $\vec{F}_1$‘de ve bitiş noktası $\vec{F}_2$‘nin ters çevrilmiş hali olan vektör, $\vec{F}_1 – \vec{F}_2$ vektörüdür.

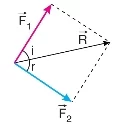
Paralelkenar Yöntemi

Paralelkenar yöntemi ile iki vektörü toplamak için, bu iki vektörün başlangıç noktaları çakışacak şekilde bir noktaya taşınır. Başlangıç noktası aynı olan vektörler, bir paralelkenar oluşturacak şekilde tamamlanır. Bu yöntemde, vektörlerin başlangıç noktalarını birleştiren köşegen, toplam vektör (bileşke vektör) olarak adlandırılır.

Paralelkenar yöntemiyle vektörlerin birleşimi şu şekildedir:

• Eğer $\vec{F}_1$ ve $\vec{F}_2$ vektörlerinin bileşkesi, şiddeti büyük olan vektöre açısal olarak daha yakındır.

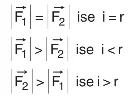
Bu yöntem, iki vektörün toplanmasında hem büyüklük hem de yönü hesaplamak için kullanılır.

Notlar:

İki kuvvetin bileşkesi, paralelkenar yöntemi ile bulunurken vektörlerin başlangıç noktaları birleştirilmelidir.

Paralelkenar yönteminde vektörlerin başlangıç noktaları birleştirilirken, uç uca ekleme yönteminde bir vektörün oku ile diğer vektörün başlangıç noktası birleştirilir.

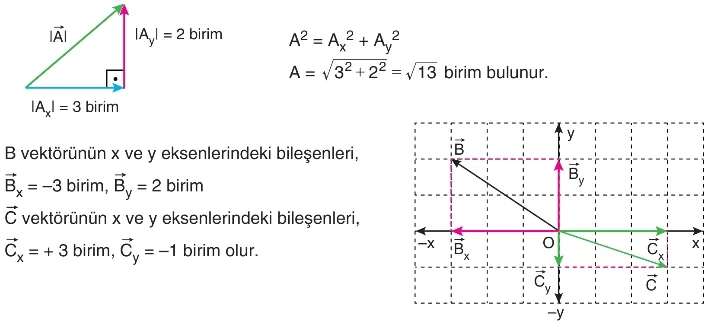
Vektörlerin Dik Bileşenlerine Ayrılması

Birimkarelere bölünmüş düzlemde, $\vec{A}$ vektörü x ve y eksenlerindeki bileşenlerine ayrılabilir. $\vec{A}$ vektörünü oluşturan bu eksenler üzerindeki vektörler, vektörün bileşenleridir. $\vec{A}$ vektörünün ucundan x ve y eksenlerine dik çizildiğinde, eksen kesen noktaların orijine uzaklıkları $\vec{A_x}$ ve $\vec{A_y}$ bileşenleridir.

Örneğin:

• $\vec{A_x}$ vektörünün x eksenindeki büyüklüğü 3 birim,
• $\vec{A_y}$ vektörünün y eksenindeki büyüklüğü 2 birimdir.

Vektörün dik bileşenleri kullanılarak, $\vec{A}$ vektörünün büyüklüğü pisagor teoremi ile bulunabilir. Bileşenler birbirine dik olduğu için:

$$\vec{A} = \vec{A_x} + \vec{A_y}$$

​

Fizik, doğadaki olayları anlamak ve açıklamak için matematiksel ve kavramsal araçlar kullanır. Bu araçların en önemlilerinden biri, vektörlerdir. Vektörler, hem büyüklük hem de yön bilgisi içeren fiziksel niceliklerdir. Birçok fiziksel olay ve büyüklük, vektörler aracılığıyla tanımlanır. Vektörlerin toplanması ve bileşke vektörün bulunması, fiziksel olayların ve kuvvetlerin analizinde önemli bir rol oynar.

Vektörlerin Tanımı ve Özellikleri

Vektörler, iki temel bileşenden oluşur: büyüklük ve yön. Bir vektörün büyüklüğü, uzunluğu ile temsil edilir ve vektörün ne kadar büyük olduğunu gösterir. Yön ise, vektörün hangi yöne doğru olduğunu ifade eder. Vektörler, genellikle oklarla gösterilir; okun uzunluğu büyüklüğü, oku yönü ise vektörün yönünü belirtir. Örneğin, kuvvet, hız, yer değiştirme ve ivme gibi büyüklükler vektörel büyüklüklerdir.

Vektörlerin Toplanması

Vektörlerin toplanması, iki veya daha fazla vektörün birleşerek tek bir vektör oluşturması işlemidir. Bu işlem, vektörlerin bileşenlerinin toplanmasıyla gerçekleştirilir ve sonuç olarak elde edilen vektöre "bileşke vektör" denir. Vektörlerin toplanması, fiziksel olayların ve kuvvetlerin net etkilerini belirlemek için kullanılır.

Uç Uca Ekleme Yöntemi

Uç uca ekleme yöntemi, vektörlerin toplanmasında kullanılan temel yöntemlerden biridir. Bu yöntemde, bir vektörün sonuna diğer vektörün başlangıcı eklenir. Elde edilen yeni vektör, bileşke vektörü temsil eder.

Adımlar:

• Birinci vektörün başlangıç noktasını belirleyin ve vektörü çizin.
• İkinci vektörün başlangıç noktasını, birinci vektörün bitiş noktasına yerleştirin ve vektörü çizin.
• Başlangıç noktasından bitiş noktasına doğru bir vektör çizerek bileşke vektörü elde edin.

Bu yöntem, vektörlerin grafiksel olarak toplanmasında kullanılır ve vektörlerin yön ve büyüklüklerini görselleştirmeyi sağlar.

Örnek: İki vektör A ve B'nin bileşkesini bulmak için, A vektörünü çizin ve B vektörünü A vektörünün bitiş noktasına ekleyin. A ve B vektörlerinin birleştiği noktadan başlayarak, başlangıç noktasına doğru bir vektör çizerek bileşke vektörü elde edin.

Paralelkenar Yöntemi

Paralelkenar yöntemi, vektörlerin toplanmasında kullanılan bir diğer yöntemdir. Bu yöntemde, iki vektörün başlangıç noktaları birleştirilir ve bir paralelkenar oluşturulur. Paralelkenarın köşegenleri, vektörlerin bileşkesini temsil eder.

Adımlar:

• İki vektörün başlangıç noktalarını birleştirin ve vektörleri çizin.
• Her iki vektörün yönünde paralel çizgiler çizerek bir paralelkenar oluşturun.
• Paralelkenarın köşegenini çizerek bileşke vektörü elde edin.

Bu yöntem, vektörlerin grafiksel olarak toplanmasında kullanılan etkili bir yöntemdir ve vektörlerin bileşenlerini görselleştirmeyi sağlar.

Örnek: İki vektör A ve B'nin bileşkesini bulmak için, A ve B vektörlerini başlangıç noktalarından çizin. A vektörüne paralel bir çizgi ve B vektörüne paralel bir çizgi çizerek bir paralelkenar oluşturun. Paralelkenarın köşegenini çizerek bileşke vektörü elde edin.

Bileşenlere Ayırma Yöntemi

Bileşenlere ayırma yöntemi, vektörlerin analitik olarak toplanmasında kullanılır. Bu yöntemde, vektörler yatay (x ekseni) ve dikey (y ekseni) bileşenlerine ayrılır ve bileşenler ayrı ayrı toplanır.

Adımlar:

• Her vektörü yatay ve dikey bileşenlerine ayırın.
• Yatay bileşenleri (x bileşenleri) toplayarak toplam yatay bileşeni bulun.
• Dikey bileşenleri (y bileşenleri) toplayarak toplam dikey bileşeni bulun.
• Toplam yatay ve dikey bileşenleri kullanarak bileşke vektörü hesaplayın.

Bu yöntem, vektörlerin büyüklük ve yönlerini hesaplamada kullanılır ve özellikle karmaşık vektörlerin toplanmasında etkilidir.

Örnek: İki vektör A ve B'nin bileşkesini bulmak için, A ve B vektörlerini yatay ve dikey bileşenlerine ayırın. Yatay bileşenleri toplayarak toplam yatay bileşeni (Rx) ve dikey bileşenleri toplayarak toplam dikey bileşeni (Ry) bulun. Bileşke vektörün büyüklüğünü ve yönünü hesaplamak için Pythagoras teoremi ve trigonometrik fonksiyonlar kullanın.

Vektörlerin toplanması ve bileşke vektörün bulunması, fiziğin temel konularından biridir ve birçok fiziksel olayın analizinde kullanılır. Uç uca ekleme, paralelkenar ve bileşenlere ayırma yöntemleri, vektörlerin toplanmasında kullanılan başlıca yöntemlerdir. Bu yöntemlerin doğru bir şekilde anlaşılması, öğrencilerin fiziksel olayları daha iyi kavramalarını ve bilimsel düşünme becerilerini geliştirmelerini sağlar. 9. sınıf fizik dersinde vektörlerin toplanması ve bileşke vektör konusunun öğrenilmesi, ileri düzey fizik konularının temelini oluşturur ve öğrencilerin fiziksel dünyayı anlamalarına yardımcı olur.