Vektörlerin Toplanması

Birden fazla vektörün toplanmasıyla elde edilen vektöre “bileşke vektör” denir. Bileşke vektör, $\vec{R}$ sembolü ile ifade edilir ve farklı yöntemlerle hesaplanabilir.

Uç Uca Ekleme Yöntemi
Vektörlerin özellikleri değişmeksizin, bir vektörün bitiş noktası diğer vektörün başlangıç noktasına eklenir. İlk vektörün başlangıç noktası ile son vektörün bitiş noktası arasında oluşan vektör, bileşke vektördür.

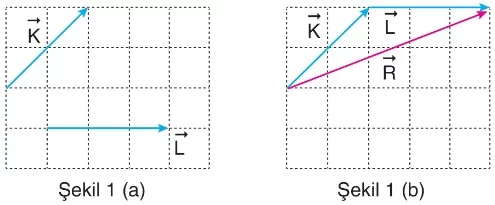
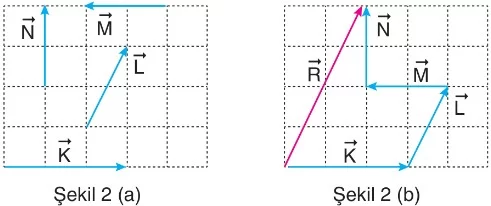
Şekil 1’de, $\vec{K}$ ve $\vec{L}$ vektörlerinin bileşkesi gösterilmektedir. Şekil 1(b)’deki $\vec{R} = \vec{K} + \vec{L}$ ifadesi, bu vektörlerin toplanması sonucunda elde edilen bileşke vektördür.

Şekil 2’de ise daha fazla vektörün bileşkesi hesaplanmaktadır. Tüm vektörler uç uca eklenerek bileşke vektör elde edilir. İlk vektörün başlangıç noktası ile son vektörün bitiş noktası arasında çizilen vektör, bu vektörlerin bileşkesi olur.

Şekil 2(a) ve 2(b) arasında gösterilen $\vec{K}, \vec{L}, \vec{M}, \vec{N}$ vektörlerinin toplamı yine $\vec{R}$ ile gösterilmektedir.

Vektörlerde Çıkarma İşlemi
Vektörlerin çıkarılması, çıkarılacak vektörün ters çevrilip diğer vektörle birleştirilmesiyle yapılır. Şekil 1(a)’da, $\vec{K}$ ve $\vec{L}$ vektörlerinin farkı bulunurken, $\vec{L}$ vektörü ters çevrilip $\vec{K}$ vektörüne eklenir. Bu işlem, toplama işlemine benzetilerek yapılır. Şekil 1(b)’de, $\vec{R} = \vec{K} + (-\vec{L})$ şeklinde gösterilen bileşke vektör elde edilir.

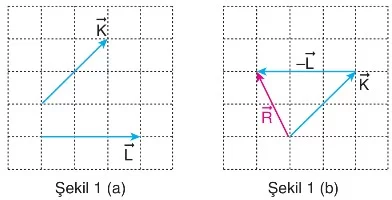
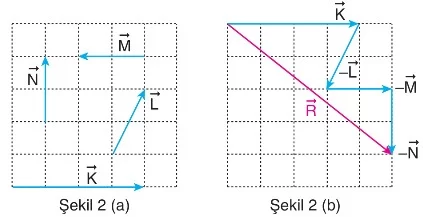
Şekil 2(a)’da $\vec{K}, \vec{L}, \vec{M}, \vec{N}$ vektörleri verilmiştir. Vektörlerin bileşkesi bulunurken, ters işaretli vektörler varsa bunlar ters çevrilip uç uca eklenerek bileşke vektör bulunur. Örneğin, $\vec{K}, -\vec{L}, -\vec{M}, -\vec{N}$ vektörlerinin bileşkesi şu şekilde hesaplanır:

$\vec{R} = \vec{K} + (-\vec{L}) + (-\vec{M}) + (-\vec{N})$

Şekil 2(b)’de gösterilen vektör $\vec{R}$ bileşkesi olarak elde edilir.

Vektörlerin Paralelkenar Yöntemi ile Toplanması
Vektörlerin bileşkesi, paralelkenar yöntemiyle de bulunabilir. Şekildeki vektörlerin büyüklükleri ve yönleri değiştirilmeden, başlangıç noktaları birleştirilir ve şekil bir paralelkenar oluşturacak şekilde tamamlanır. Başlangıç noktası ile bitiş noktası arasındaki köşe boyunca oluşan vektör, bileşke vektördür.

Şekil 1(a)’da $\vec{K}$ ve $\vec{L}$ vektörlerinin bileşkesi $\vec{R} = \vec{K} + \vec{L}$ olarak ifade edilmiştir. Şekil 1(b)’de de bu bileşke vektör gösterilmektedir.

Şekil 2(a)’da, büyüklükleri ve yönleri değiştirilmeden birleştirilen vektörlerin başlangıç noktaları O’da buluşturulur ve paralelkenar yöntemiyle bileşke vektör elde edilir. Şekil 2(b)’de, $\vec{K}$ ve $\vec{L}$ vektörlerinin bileşkesi yine $\vec{R}=\vec{K}+\stackrel{}{L}$ olarak gösterilmektedir.

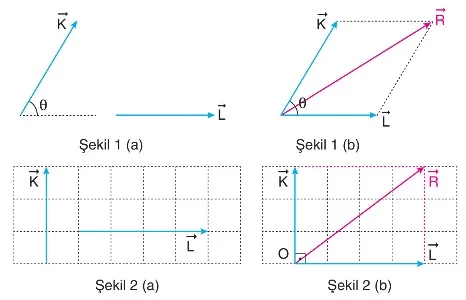
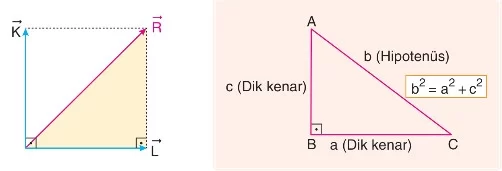
Eğer $\vec{K}$ ve $\vec{L}$ vektörleri arasındaki açı 90° ise, bileşke vektör Pisagor teoremi ile bulunur. $\vec{R}$ vektörünün büyüklüğü şu şekilde hesaplanır:

$$R^2 = K^2 + L^2$$

Vektörlerin Bileşenlerine Ayrılması
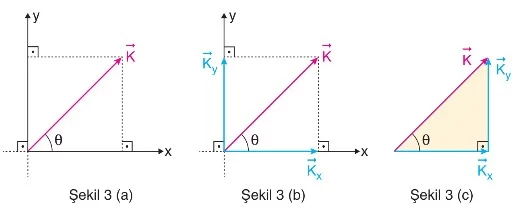
Bir vektör verildiğinde, bu vektör kartezyen koordinat sisteminde bileşenlerine ayrılabilir.

Şekil 3(a)’da gösterilen $\vec{K}$ vektörü, önce x ve y koordinat eksenlerinde ayrılır. Şekil 3(b)’de görüldüğü gibi, $\vec{K}$ vektörünün bitiş noktasından x ve y eksenlerine dik çizgiler çekilir. Böylece, vektörün x ve y eksenleri üzerindeki bileşenleri $\vec{K_x}$ ve $\vec{K_y}$ olarak gösterilir. $\vec{K}$ vektörünün büyüklüğü, şu eşitlik ile hesaplanır:

$$K^2 = K_x^2 + K_y^2$$